Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Love, E. R.
1986.
Inequalities related to those of Hardy and of Cochran and Lee.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 99,
Issue. 3,
p.
395.
Love, E. R.
1987.
General Inequalities 5.
p.
87.
Heinig, H. P.
1990.
Nonlinear Analysis, Function Spaces and Applications Vol. 4.
p.
42.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1991.
Inequalities Involving Functions and Their Integrals and Derivatives.
p.
143.
Opic, B.
and
Gurka, P.
1994.
Weighted inequalities for geometric means.
Proceedings of the American Mathematical Society,
Vol. 120,
Issue. 3,
p.
771.
Čižmešija, Aleksandra
and
Pečarić, Josip
2000.
Survey on Classical Inequalities.
p.
27.
C˘iz˘mes˘ija, Aleksandra
and
Pec˘arić, Josip
2001.
Some new generalisations of inequalities of Hardy and Levin–Cochran–Lee.
Bulletin of the Australian Mathematical Society,
Vol. 63,
Issue. 1,
p.
105.
Kaijser, Sten
Persson, Lars-Erik
and
Öberg, Anders
2002.
On Carleman and Knopp's Inequalities.
Journal of Approximation Theory,
Vol. 117,
Issue. 1,
p.
140.
Čižmešija, Aleksandra
Pečarić, Josip
and
Persson, Lars–Erik
2003.
On strengthened Hardy and Pólya–Knopp's inequalities.
Journal of Approximation Theory,
Vol. 125,
Issue. 1,
p.
74.
Čižmešija, Aleksandra
and
Perić, Ivan
2004.
Mixed means over balls and annuli and lower bounds for operator norms of maximal functions.
Journal of Mathematical Analysis and Applications,
Vol. 291,
Issue. 2,
p.
625.
2005.
Mathematical Inequalities.
Vol. 67,
Issue. ,
p.
485.
Alzer, Horst
2005.
Sharp Inequalities for the Hurwitz Zeta Function.
Rocky Mountain Journal of Mathematics,
Vol. 35,
Issue. 2,
2005.
Mathematical Inequalities.
Vol. 67,
Issue. ,
p.
565.
LUOR, DAH-CHIN
2008.
ON WEIGHTED INEQUALITIES WITH GEOMETRIC MEAN OPERATOR.
Bulletin of the Australian Mathematical Society,
Vol. 78,
Issue. 3,
p.
463.
Luor, Dah-Chin
2010.
Multidimensional Exponential Inequalities with Weights.
Canadian Mathematical Bulletin,
Vol. 53,
Issue. 2,
p.
327.
Adiyasuren, Vandanjav
Batbold, Tserendorj
and
Krnić, Mario
2015.
The Best Constants in Multidimensional Hilbert-Type Inequalities Involving Some Weighted Means Operators.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 38,
Issue. 3,
p.
1001.
Bandaliev, R. A.
2015.
Two-Weight Criteria for the Multidimensional Hardy-Type Operator in p-Convex Banach Function Spaces and Some Applications.
Ukrainian Mathematical Journal,
Vol. 67,
Issue. 3,
p.
357.
Bandaliyev, Rovshan A.
Serbetci, Ayhan
and
Hasanov, Sabir G.
2018.
On Hardy Inequality in Variable Lebesgue Spaces with Mixed Norm.
Indian Journal of Pure and Applied Mathematics,
Vol. 49,
Issue. 4,
p.
765.
Bandaliyev, R. A.
Guliyev, V. S.
and
Hasanov, S. G.
2018.
Two-Weighted Inequalities for the Riesz Potential in p-Convex Weighted Modular Banach Function Spaces.
Ukrainian Mathematical Journal,
Vol. 69,
Issue. 11,
p.
1673.
Yimer, Markos Fisseha
Persson, Lars-Erik
and
Ayele, Tsegaye Gedif
2024.
Modern Problems in PDEs and Applications.
Vol. 4,
Issue. ,
p.
185.


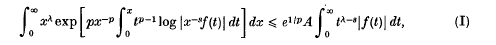
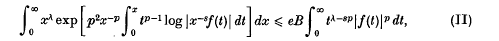
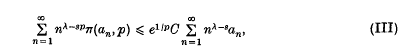
 is a sequence of nonnegative real numbers,
is a sequence of nonnegative real numbers,