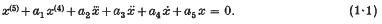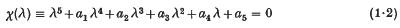Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ezeilo, J. O. C.
1979.
A further instability theorem for a certain fifth-order differential equation.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 86,
Issue. 3,
p.
491.
Ezeilo, J. O. C.
1982.
An instability theorem for a certain sixth order differential equation.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 32,
Issue. 1,
p.
129.
Wen-Jian, Li
and
Kui-chen, Duan
1995.
Instability theorems for certain nth order differential equations.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 59,
Issue. 1,
p.
1.
Sadek, A.I.
2003.
Instability results for certain systems of fourth and fifth order differential equations.
Applied Mathematics and Computation,
Vol. 145,
Issue. 2-3,
p.
541.
Tunç, Cemil
2004.
An instability result for certain system of sixth order differential equations.
Applied Mathematics and Computation,
Vol. 157,
Issue. 2,
p.
477.
Tunç, C.
and
Tunç, E.
2006.
An instability theorem for a class of eighth-order differential equations.
Differential Equations,
Vol. 42,
Issue. 1,
p.
150.
Tunç, Cemil
and
Erdogan, Fevzi
2007.
On the instability of solutions of certain non-autonomous vector differential equations of fifth order.
SUT Journal of Mathematics,
Vol. 43,
Issue. 1,
Tunç, Cemil
Karta, Melike
and
Zhang, Binggen
2008.
A New Instability Result to Nonlinear Vector Differential Equations of Fifth Order.
Discrete Dynamics in Nature and Society,
Vol. 2008,
Issue. 1,
Tunç, Cemil
2008.
ON THE INSTABILITY OF SOLUTIONS TO A CERTAIN CLASS OF NON-AUTONOMOUS AND NON-LINEAR ORDINARY VECTOR DIFFERENTIAL EQUATIONS OF SIXTH ORDER.
Albanian Journal of Mathematics,
Vol. 2,
Issue. 1,
Tunç, Cemil
2011.
An instability theorem for a certain fifth-order delay differential equation.
Filomat,
Vol. 25,
Issue. 3,
p.
145.
Tunç, Cemil
2013.
Instability of a Fifth-Order Nonlinear Vector Delay Differential Equation with Multiple Deviating Arguments.
Journal of Mathematics,
Vol. 2013,
Issue. ,
p.
1.