Article contents
Integrals with a large parameter: paths of descent and conformal mapping
Published online by Cambridge University Press: 24 October 2008
Abstract
The method of steepest descents is widely used to find the asymptotic expansion of contour integrals of the form
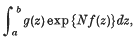
where N is a large positive parameter, and f(z) and g(z) are analytic functions of z. (For the sake of simplicity it will here be supposed that f(z) and g(z) are regular except at ∞, but our arguments can be extended to include singularities at other points.) In the method of steepest descents the path of integration is deformed into a new equivalent path consisting of the paths of steepest descent through a and b, together with paths of steepest descent through certain saddle points, the relevant saddle points. (Paths of descent, etc., are defined in §1 below.) Watson's Lemma then shows that the complete asymptotic expansion depends on the local behaviour of f(z) and g(z) at the end-points and at the relevant saddle-points. On the other hand to determine which saddle-points are relevant is a global (non-local) problem and requires either the tracing of paths of steepest descent all the way from saddle-points and endpoints to ∞, or some other global process. It has often been noted that in applications of Watson's Lemma the paths of steepest descent can be replaced by a wider class of paths of descent. In this way we are led to global problems like the following: Given 2points z = α and z = β where Nf(a) > Nf(β), can apath of descent be drawn from α to β? If also Ff(α) = Ff(β), can a path of steepest descent be drawn from α to β?
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 2 , March 1970 , pp. 371 - 381
- Copyright
- Copyright © Cambridge Philosophical Society 1970
References
REFERENCES
- 11
- Cited by

