No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Haefliger's theorem (3) that the group of isotopy classes of embeddings of Sx in Sn when n − x > 2 is isomorphic to the triad group πx+1(G; G(n − x),SO), where G(n − x) is the H-space of homotopy equivalences of Sn−x−1 of degree 1, 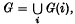 , and SO is the stable special orthogonal group, is generalized in this paper by replacing Sx and Sn by arbitrary compact connected smooth manifolds Xx, Mn without boundary. The embedding and knot problems are reduced to homotopy theory. The question of P.L. manifolds is discussed in section 4. The case Mn = Sn will be considered first; the generalization is stated in section 3.
, and SO is the stable special orthogonal group, is generalized in this paper by replacing Sx and Sn by arbitrary compact connected smooth manifolds Xx, Mn without boundary. The embedding and knot problems are reduced to homotopy theory. The question of P.L. manifolds is discussed in section 4. The case Mn = Sn will be considered first; the generalization is stated in section 3.