Published online by Cambridge University Press: 11 October 2016
We study the set 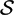 ${\mathcal{S}}$ of labelled seeds of a cluster algebra of rank n inside a field
${\mathcal{S}}$ of labelled seeds of a cluster algebra of rank n inside a field 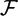 ${\mathcal{F}}$ as a homogeneous space for the group Mn of (globally defined) mutations and relabellings. Regular equivalence relations on
${\mathcal{F}}$ as a homogeneous space for the group Mn of (globally defined) mutations and relabellings. Regular equivalence relations on 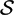 ${\mathcal{S}}$ are associated to subgroups W of AutMn(
${\mathcal{S}}$ are associated to subgroups W of AutMn(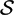 ${\mathcal{S}}$), and we thus obtain groupoids W\
${\mathcal{S}}$), and we thus obtain groupoids W\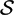 ${\mathcal{S}}$. We show that for two natural choices of equivalence relation, the corresponding groups Wc and W+ act on
${\mathcal{S}}$. We show that for two natural choices of equivalence relation, the corresponding groups Wc and W+ act on 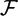 ${\mathcal{F}}$, and the groupoids Wc\
${\mathcal{F}}$, and the groupoids Wc\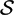 ${\mathcal{S}}$ and W+\
${\mathcal{S}}$ and W+\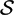 ${\mathcal{S}}$ act on the model field
${\mathcal{S}}$ act on the model field 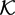 ${\mathcal{K}}$=ℚ(x1,. . .,xn). The groupoid W+\
${\mathcal{K}}$=ℚ(x1,. . .,xn). The groupoid W+\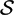 ${\mathcal{S}}$ is equivalent to Fock–Goncharov's cluster modular groupoid. Moreover, Wc is isomorphic to the group of cluster automorphisms, and W+ to the subgroup of direct cluster automorphisms, in the sense of Assem–Schiffler–Shramchenko.
${\mathcal{S}}$ is equivalent to Fock–Goncharov's cluster modular groupoid. Moreover, Wc is isomorphic to the group of cluster automorphisms, and W+ to the subgroup of direct cluster automorphisms, in the sense of Assem–Schiffler–Shramchenko.
We also prove that, for mutation classes whose seeds have mutation finite quivers, the stabiliser of a labelled seed under Mn determines the quiver of the seed up to ‘similarity’, meaning up to taking opposites of some of the connected components. Consequently, the subgroup Wc is the entire automorphism group of 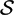 ${\mathcal{S}}$ in these cases.
${\mathcal{S}}$ in these cases.