Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T09:03:54.670Z Has data issue: false hasContentIssue false
  • English
  • Français

(LF)-spaces with absolute bases

Published online by Cambridge University Press:  24 October 2008

G. Bennett  and
J. B. Cooper
G. Bennett
Affiliation:
St John's College, Cambridge
J. B. Cooper
Affiliation:
Clare College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose E is a locally convex space over a field K which can be the real line or the complex plane. Then a basis for E is a sequence (xk) of elements of E such that, if x ∈ E, x can be expressed uniquely as

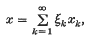
where ξk ∈K for each k. If this representation converges absolutely, i.e. if

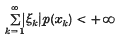
for every continuous seminorm p on E, then (xk) is called an absolute basis for E. If the mappings x → ξk from E into K are continuous for each k, then (xk) is a Schauder basis for E. The purpose of this paper is to prove some results for (LF)-spaces with bases and to use them to extend some theorems due to Pietsch. We recall that an (F)-space is a complete metrizable locally convex space and an (LF)-space the inductive limit of a strictly increasing sequence of (F)-spaces (En, τn) such that τn+1|En = τn for all n.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 2 , March 1970 , pp. 283 - 286
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Arsove, M. G. and Edwards, R. E.Generalized bases in topological linear spaces. Studia Math. 19 (1960), 95–113.CrossRefGoogle Scholar
(2)Bennett, G. and Cooper, J. B. Weak bases in (F)- and (LF)-spaces. To appear in J. London Math. Soc.Google Scholar
(3)Dieudonné, J. and Schwartz, L.La dualité dans les espaces (F) et (LF) Ann. Inst. Fourier (Grenoble) 1 (1949), 61–101.CrossRefGoogle Scholar
(4)Grothendieck, A.Produits tensoriels topologiques et espaces nucléaires. Memoirs of the Amer. Math. Soc. (1955).CrossRefGoogle Scholar
(5)Pietsch, A.(F)-Räume mit absoluter Basis. Studia Math. 26 (1966), 233–238.CrossRefGoogle Scholar
(6)Robertson, A. P. and Robertson, W. J.Topological vector spaces (Cambridge, 1964).Google Scholar