Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cohn, P. M.
1955.
A non-nilpotent Lie ring satisfying the Engel condition and a non-nilpotent Engel group.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 51,
Issue. 3,
p.
401.
Higman, Graham
1956.
On finite groups of exponent five.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 52,
Issue. 3,
p.
381.
Davis, Robert L.
1959.
Torsion in Engel modules.
Proceedings of the American Mathematical Society,
Vol. 10,
Issue. 5,
p.
679.
Heineken, Hermann
1962.
Endomorphismenringe und engelsche Elemente.
Archiv der Mathematik,
Vol. 13,
Issue. 1,
p.
29.
Heineken, Hermann
1963.
Liesche Ringe mit Engelbedingung.
Mathematische Annalen,
Vol. 149,
Issue. 3,
p.
232.
Kuz'min, E. N.
1967.
On anticommutative algebras satisfying the engel condition.
Siberian Mathematical Journal,
Vol. 8,
Issue. 5,
p.
779.
Bakhturin, Yu. A.
1968.
Two remarks on varieties of Lie algebras.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 4,
Issue. 4,
p.
725.
Bachmuth, Seymour
Mochizuki, Horace Y.
and
Walkup, David
1970.
A nonsolvable group of exponent 5.
Bulletin of the American Mathematical Society,
Vol. 76,
Issue. 3,
p.
638.
Putcha, Mohan S.
1971.
On Lie rings satisfying the fourth Engel condition.
Proceedings of the American Mathematical Society,
Vol. 28,
Issue. 2,
p.
355.
Razmyslov, Yu. P.
1971.
On Lie algebras satisfying the Engel condition.
Algebra and Logic,
Vol. 10,
Issue. 1,
p.
21.
Bachmuth, S.
and
Mochizuki, H.Y.
1971.
Third Engel groups and the Macdonald-Neumann conjecture.
Bulletin of the Australian Mathematical Society,
Vol. 5,
Issue. 3,
p.
379.
Razmyslov, Yu. P.
1972.
An example of unsolvable just non-cross varieties of groups.
Algebra and Logic,
Vol. 11,
Issue. 2,
p.
108.
Bachmuth, S.
Mochizuki, H.Y.
and
Walkup, D.W.
1973.
Word Problems - Decision Problems and the Burnside Problem in Group Theory.
Vol. 71,
Issue. ,
p.
39.
Kostrikin, A. I.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
409.
Kostrikin, A. I.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
409.
Filippov, V. T.
1975.
Mal'cev algebras satisfying Engel's condition.
Algebra and Logic,
Vol. 14,
Issue. 4,
p.
271.
Khukhro, E. I.
1978.
A solvable group admitting a regular splitting automorphism of prime order is nilpotent.
Algebra and Logic,
Vol. 17,
Issue. 5,
p.
402.
Kawamoto, Naoki
1979.
Subideality and ascendancy in generalized solvable Lie algebras.
Hiroshima Mathematical Journal,
Vol. 9,
Issue. 3,
Filippov, V. T.
1980.
Finitely generated Mal'tsev algebras.
Algebra and Logic,
Vol. 19,
Issue. 4,
p.
311.
Khukhro, E. I.
1980.
Nilpotency of solvable groups admitting a splitting automorphism of prime order.
Algebra and Logic,
Vol. 19,
Issue. 1,
p.
77.
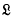 be a Lie ring in which the product of elements x and y is denoted by xy. The inner derivations of
be a Lie ring in which the product of elements x and y is denoted by xy. The inner derivations of 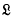 , i.e. the mappings X:a→ax for fixed elements x of
, i.e. the mappings X:a→ax for fixed elements x of 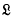 , form a Lie ring
, form a Lie ring 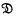 under the product [X, Y] = XY – YX, and the mapping x→ X is a homo-morphism of
under the product [X, Y] = XY – YX, and the mapping x→ X is a homo-morphism of 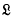 onto
onto 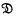 . We shall say that
. We shall say that 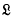 satisfies the nth Engel condition if Xn = 0 for all X in
satisfies the nth Engel condition if Xn = 0 for all X in 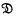 , i.e. if
, i.e. if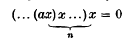
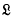 . If
. If 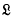 satisfies the maximum condition on subrings, it is known (1) that this condition implies the nilpotence of
satisfies the maximum condition on subrings, it is known (1) that this condition implies the nilpotence of 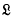 ; indeed,
; indeed, 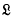 must then be nilpotent even if the integer n is allowed to depend on the element X of
must then be nilpotent even if the integer n is allowed to depend on the element X of 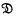 . We consider here the case in which n is independent of X but
. We consider here the case in which n is independent of X but 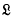 does not necessarily satisfy the maximum condition, and inquire whether
does not necessarily satisfy the maximum condition, and inquire whether 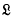 is then nilpotent.
is then nilpotent.