No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Definition (Moukoko Priso(2)). A locally convex spaceE[T] is said to have a strict absorbent network of type Σ if there exists in E a family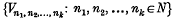 of absolutely convex absorbent sets such that
of absolutely convex absorbent sets such that
(1) if {nk} is a sequence of positive integers and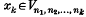 for each k, then the series
for each k, then the series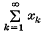 converges in E[T]
converges in E[T]
(2) for each sequence {nk} there is a sequence {λk} of positive real numbers such that, if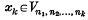 and 0 ≤ μk ≤ λkfor each k, then
and 0 ≤ μk ≤ λkfor each k, then
(i) 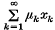 converges in E[T], and
converges in E[T], and
(ii) 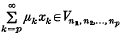 for each p.
for each p.