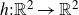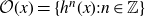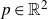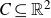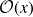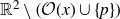1. Introduction
Given a set D by
![]() $\mathrm{cl}(D),\mathrm{int}(D)$
, and
$\mathrm{cl}(D),\mathrm{int}(D)$
, and
![]() $\partial D$
we shall denote the closure, interior and boundary of D respectively.
$\partial D$
we shall denote the closure, interior and boundary of D respectively.
![]() $\mathbb{S}^n$
denotes the n-dimensional sphere, and
$\mathbb{S}^n$
denotes the n-dimensional sphere, and
![]() $\mathbb{R}^2$
denotes the plane. Given an orientation preserving homeomorphism
$\mathbb{R}^2$
denotes the plane. Given an orientation preserving homeomorphism
![]() $h\,:\,\mathbb{R}^2\to\mathbb{R}^2$
the orbit of x is given by
$h\,:\,\mathbb{R}^2\to\mathbb{R}^2$
the orbit of x is given by
![]() $\mathcal{O}(x)=\{h^n(x)\,:\,n\in\mathbb{Z}\}$
. This paper is concerned with the existence of fixed points of orientation preserving homeomorphisms of
$\mathcal{O}(x)=\{h^n(x)\,:\,n\in\mathbb{Z}\}$
. This paper is concerned with the existence of fixed points of orientation preserving homeomorphisms of
![]() $\mathbb{R}^2$
linked to bounded orbits, in the sense introduced by J.-M. Gambaudo in [
Reference Gambaudo11
]. Let
$\mathbb{R}^2$
linked to bounded orbits, in the sense introduced by J.-M. Gambaudo in [
Reference Gambaudo11
]. Let
![]() $\mathcal{O}_1$
and
$\mathcal{O}_1$
and
![]() $\mathcal{O}_2$
be two sets invariant for a homeomorphism h. Following [
Reference Gambaudo11
] we say that these two sets are unlinked if there exist two discs
$\mathcal{O}_2$
be two sets invariant for a homeomorphism h. Following [
Reference Gambaudo11
] we say that these two sets are unlinked if there exist two discs
![]() $D_1,D_2\subset \mathbb{R}^2$
with the following properties:
$D_1,D_2\subset \mathbb{R}^2$
with the following properties:
-
(1)
 $\mathcal{O}_i\subset \mathrm{int}(D_i)$
for i=1,2;
$\mathcal{O}_i\subset \mathrm{int}(D_i)$
for i=1,2; -
(2)
 $D_1\cap D_2=\emptyset$
;
$D_1\cap D_2=\emptyset$
; -
(3)
 $h(\partial D_i)$
is isotopic to
$h(\partial D_i)$
is isotopic to
 $\partial D_i$
in
$\partial D_i$
in
 $\mathbb{R}^2\setminus\left(\mathcal{O}_1\cup\mathcal{O}_2\right)$
, for
$\mathbb{R}^2\setminus\left(\mathcal{O}_1\cup\mathcal{O}_2\right)$
, for
 $i=1,2$
.
$i=1,2$
.
Note that if
![]() $\mathrm{cl}(\mathcal{O}_1)\cap\mathcal{O}_2\neq\emptyset$
then
$\mathrm{cl}(\mathcal{O}_1)\cap\mathcal{O}_2\neq\emptyset$
then
![]() $\mathcal{O}_1$
and
$\mathcal{O}_1$
and
![]() $\mathcal{O}_2$
are linked in a trivial way, as there is no Jordan curve around
$\mathcal{O}_2$
are linked in a trivial way, as there is no Jordan curve around
![]() $\mathcal{O}_2$
separating the two sets. Gambaudo showed that for any
$\mathcal{O}_2$
separating the two sets. Gambaudo showed that for any
![]() $C^1$
-embedding f of a disk, and any periodic orbit O of f, there exists a fixed point p linked to O. As a consequence, for the torus flow
$C^1$
-embedding f of a disk, and any periodic orbit O of f, there exists a fixed point p linked to O. As a consequence, for the torus flow
![]() $\phi_t$
suspending f, the sets
$\phi_t$
suspending f, the sets
![]() $\{\phi_t(O)\}_{\geq 0}$
and
$\{\phi_t(O)\}_{\geq 0}$
and
![]() $\{\phi_t(p)\}_{\geq 0}$
are linked as knots in
$\{\phi_t(p)\}_{\geq 0}$
are linked as knots in
![]() $\mathbb{S}^3$
. A similar result was obtained simultaneously by B. Kolev in [
Reference Kolev14
], who showed linking of a periodic orbit to a fixed point for orientation preserving
$\mathbb{S}^3$
. A similar result was obtained simultaneously by B. Kolev in [
Reference Kolev14
], who showed linking of a periodic orbit to a fixed point for orientation preserving
![]() $C^1$
-diffeomorphisms of
$C^1$
-diffeomorphisms of
![]() $\mathbb{R}^2$
. The result of Gambaudo and Kolev was generalised to orientation reversing homeomorphisms of
$\mathbb{R}^2$
. The result of Gambaudo and Kolev was generalised to orientation reversing homeomorphisms of
![]() $\mathbb{S}^2$
by M. Bonino [
Reference Bonino1
], who showed linking of periodic orbits of period at least 3, to periodic orbits of least period 2. Bonino also pointed out that Kolev’s proof, in the orientation preserving case, works in
$\mathbb{S}^2$
by M. Bonino [
Reference Bonino1
], who showed linking of periodic orbits of period at least 3, to periodic orbits of least period 2. Bonino also pointed out that Kolev’s proof, in the orientation preserving case, works in
![]() $C^0$
as well, as it is enough to perturb a given homeomorphism slightly, by smoothing it out in a small neighbourhood of the periodic orbit and then apply the same proof. In the present paper we improve on the results of Gambaudo and Kolev, by proving that any bounded orbit is linked to a fixed point.
$C^0$
as well, as it is enough to perturb a given homeomorphism slightly, by smoothing it out in a small neighbourhood of the periodic orbit and then apply the same proof. In the present paper we improve on the results of Gambaudo and Kolev, by proving that any bounded orbit is linked to a fixed point.
Theorem 1·1. Let
![]() $h\,:\,\mathbb{R}^2 \to \mathbb{R}^2$
be an orientation preserving homeomorphism. For any bounded orbit
$h\,:\,\mathbb{R}^2 \to \mathbb{R}^2$
be an orientation preserving homeomorphism. For any bounded orbit
![]() $\mathcal{O}(x)$
there exists a fixed point
$\mathcal{O}(x)$
there exists a fixed point
![]() $p\in\mathbb{R}^2$
linked to
$p\in\mathbb{R}^2$
linked to
![]() $\mathcal{O}(x)$
.
$\mathcal{O}(x)$
.
Outline of Proof.
-
(i) Suppose no point in
 $\mathrm{Fix}(h)$
is linked to the compact
$\mathrm{Fix}(h)$
is linked to the compact
 $K=\mathrm{cl}\mathcal{O}(x)$
.
$K=\mathrm{cl}\mathcal{O}(x)$
. -
(ii) Then there exists a lift
 $\tilde{h}$
of h to the universal cover
$\tilde{h}$
of h to the universal cover
 $(\tau,\tilde{U})$
of an open surface U (which is the component of
$(\tau,\tilde{U})$
of an open surface U (which is the component of
 $\mathbb{R}^2\setminus\mathrm{Fix}(h)$
containing K), and a (compact) sheet
$\mathbb{R}^2\setminus\mathrm{Fix}(h)$
containing K), and a (compact) sheet
 $\tilde{K}$
over K, such that
$\tilde{K}$
over K, such that
 $\tilde{h}(\tilde K)=\tilde K$
. This step is possible since
$\tilde{h}(\tilde K)=\tilde K$
. This step is possible since
 $h(U)=U$
, as a consequence of a result of Brown and Kister [
Reference Brown and Kister6
].
$h(U)=U$
, as a consequence of a result of Brown and Kister [
Reference Brown and Kister6
]. -
(iii) Since
 $\tilde{h}$
is orientation preserving and fixed point free, and
$\tilde{h}$
is orientation preserving and fixed point free, and
 $\tilde K$
is compact, we obtain a contradiction with Brouwer Translation Theorem.
$\tilde K$
is compact, we obtain a contradiction with Brouwer Translation Theorem. -
(iv) To show that
 $\tilde{K}$
is invariant under
$\tilde{K}$
is invariant under
 $\tilde{h}$
, one projects
$\tilde{h}$
, one projects
 $\tilde{K}$
from the universal cover onto an infinite cyclic covering space, to realise that
$\tilde{K}$
from the universal cover onto an infinite cyclic covering space, to realise that
 $\tilde K$
is
$\tilde K$
is
 $\tilde{h}$
-invariant unless a fixed point of h linked to K already exists.
$\tilde{h}$
-invariant unless a fixed point of h linked to K already exists.
Our proof is inspired by M. Brown’s paper [
Reference Brown5
], the writing of [
Reference Boroński2
], and motivated by [
Reference Kuperberg15
] where Brown’s approach was used to show existence of periodic points in neighbourhoods of adding machines in the plane. Unlike the proofs of results in [
Reference Bonino1
], [
Reference Gambaudo11
] and [
Reference Kolev14
], our proof does not employ any elements of the Nielsen–Thurston theory, but purely topological arguments concerning covering spaces of open surfaces. We believe that this proof reveals a deeper explanation of the phenomenon described by the result of Gambaudo and Kolev. Our result is applicable not only to periodic orbits, but also to non-periodic bounded orbits, and can be used, for example, to guarantee fixed points linked to an invariant Cantor set
![]() $C=\mathrm{cl}(\mathcal{O}(x))$
. This is particularly useful when
$C=\mathrm{cl}(\mathcal{O}(x))$
. This is particularly useful when
![]() $h|C$
is minimalFootnote 2, or more generally aperiodicFootnote 3, as then C does not contain any fixed points. It is easy to find examples of local dynamics of h for which h may be such that the result of Kolev and Gambaudo does not guarantee a linked fixed point, but the above theorem does. In particular this may occur for a disk
$h|C$
is minimalFootnote 2, or more generally aperiodicFootnote 3, as then C does not contain any fixed points. It is easy to find examples of local dynamics of h for which h may be such that the result of Kolev and Gambaudo does not guarantee a linked fixed point, but the above theorem does. In particular this may occur for a disk
![]() $D\subseteq \mathbb{R}^2$
such that
$D\subseteq \mathbb{R}^2$
such that
![]() $h|\partial D$
is conjugate to a circle homeomorphism with irrational rotation number (minimal or Denjoy-type), or
$h|\partial D$
is conjugate to a circle homeomorphism with irrational rotation number (minimal or Denjoy-type), or
![]() $h|C$
is an odometer with
$h|C$
is an odometer with
![]() $C\subseteq D$
. However, the set of minimal homeomorphisms of the Cantor set is very rich, and contains homeomorphisms with any prescribed topological entropy, even topologically mixing [
Reference Lehrer18
], and so potential applications go far beyond these two examplesFootnote 4. Moreover, our result also applies to orbits whose closures might be connected sets, even separating plane continua. Finally, our theorem can also be used to detect linking of one-dimensional invariant sets of suspension flows in
$C\subseteq D$
. However, the set of minimal homeomorphisms of the Cantor set is very rich, and contains homeomorphisms with any prescribed topological entropy, even topologically mixing [
Reference Lehrer18
], and so potential applications go far beyond these two examplesFootnote 4. Moreover, our result also applies to orbits whose closures might be connected sets, even separating plane continua. Finally, our theorem can also be used to detect linking of one-dimensional invariant sets of suspension flows in
![]() $\mathbb{S}^3$
, more general than just knots considered in [
Reference Gambaudo11
], such as 1-dimensional matchbox manifolds; i.e. the class of compact connected metrisable spaces in which every point has a neighbourhood homeomorphic to the product
$\mathbb{S}^3$
, more general than just knots considered in [
Reference Gambaudo11
], such as 1-dimensional matchbox manifolds; i.e. the class of compact connected metrisable spaces in which every point has a neighbourhood homeomorphic to the product
![]() $[0,1]\times C$
. This class of spaces includes many familiar examples from the dynamics literature, such as Denjoy exceptional minimal sets of flows [
Reference Schweitzer21
], solenoids [
Reference Smale23
], and DA-attractors [
Reference Katok and Hasselblatt13
]; see e.g. [
Reference Clark, Hurder and Lukina9
] and [
Reference Fokkink10
] to learn more.
$[0,1]\times C$
. This class of spaces includes many familiar examples from the dynamics literature, such as Denjoy exceptional minimal sets of flows [
Reference Schweitzer21
], solenoids [
Reference Smale23
], and DA-attractors [
Reference Katok and Hasselblatt13
]; see e.g. [
Reference Clark, Hurder and Lukina9
] and [
Reference Fokkink10
] to learn more.
2. Proof of Theorem 1·1
Suppose
![]() $\mathcal{O}_1=\{h^n(x)\,:\,n\in\mathbb{Z}\}$
is an orbit and
$\mathcal{O}_1=\{h^n(x)\,:\,n\in\mathbb{Z}\}$
is an orbit and
![]() $\mathcal{O}_2=\{p\}$
is a fixed point of h, such that
$\mathcal{O}_2=\{p\}$
is a fixed point of h, such that
![]() $p\notin \mathrm{cl}(\mathcal{O}_1)$
. If
$p\notin \mathrm{cl}(\mathcal{O}_1)$
. If
![]() $D_2$
is a sufficiently small disk containing
$D_2$
is a sufficiently small disk containing
![]() $\mathcal{O}_2$
then
$\mathcal{O}_2$
then
![]() $\partial D_2$
is always isotopic to
$\partial D_2$
is always isotopic to
![]() $h(\partial D_2)$
Footnote 5. Therefore for linking of orbits to fixed points, Gambaudo’s definition reduces to the following condition:
$h(\partial D_2)$
Footnote 5. Therefore for linking of orbits to fixed points, Gambaudo’s definition reduces to the following condition:
-
 $\mathcal{O}_1$
and p are linked if there does not exist a closed disk
$\mathcal{O}_1$
and p are linked if there does not exist a closed disk
 $D_1$
with
$D_1$
with
 $\mathcal{O}_1\subset\mathrm{int}(D_1)$
, such that
$\mathcal{O}_1\subset\mathrm{int}(D_1)$
, such that
 $p\notin D_1$
and
$p\notin D_1$
and
 $\partial D_1$
is isotopic to
$\partial D_1$
is isotopic to
 $h(\partial D_1)$
in
$h(\partial D_1)$
in
 $\mathbb{R}^2\setminus\left(\mathcal{O}_1\cup\{p\}\right)$
.
$\mathbb{R}^2\setminus\left(\mathcal{O}_1\cup\{p\}\right)$
.
If such a Jordan curve
![]() $\partial D_1$
does exist, and consequently
$\partial D_1$
does exist, and consequently
![]() $\mathcal{O}_1$
and p are unlinked, then we shall call
$\mathcal{O}_1$
and p are unlinked, then we shall call
![]() $\partial D_1$
an unlinking of
$\partial D_1$
an unlinking of
![]() $\mathcal{O}_1$
and p.
$\mathcal{O}_1$
and p.
Recall that if U is an open surface and
![]() $(\tilde{U},\tau)$
is its universal covering space then given a homeomorphism
$(\tilde{U},\tau)$
is its universal covering space then given a homeomorphism
![]() $h\,:\,U\to U$
there exists a lift homeomorphism
$h\,:\,U\to U$
there exists a lift homeomorphism
![]() $\tilde{h}\,:\,\tilde{U}\to \tilde{U}$
such that the following diagram commutes.
$\tilde{h}\,:\,\tilde{U}\to \tilde{U}$
such that the following diagram commutes.

Additionally if
![]() $h(x)=y$
then
$h(x)=y$
then
![]() $\tilde{h}$
is uniquely determined by the choice of two points
$\tilde{h}$
is uniquely determined by the choice of two points
![]() $\tilde{x}\in\tau^{-1}(x)$
,
$\tilde{x}\in\tau^{-1}(x)$
,
![]() $\tilde{y}\in\tau^{-1}(y)$
and setting
$\tilde{y}\in\tau^{-1}(y)$
and setting
![]() $\tilde{h}(\tilde{x})=\tilde{y}$
. If
$\tilde{h}(\tilde{x})=\tilde{y}$
. If
![]() $D\subset U$
is a disk (or its subset), then
$D\subset U$
is a disk (or its subset), then
![]() $\tau^{-1}(D)$
consists of pairwise disjoint homeomorphic copies of D in
$\tau^{-1}(D)$
consists of pairwise disjoint homeomorphic copies of D in
![]() $\tilde{U}$
, called sheets. We shall need the following celebrated result of Brouwer. Brouwer’s theorem with its subsequent generalisations is much stronger, but we shall only need the weaker version stated below. The reader is referred to [
Reference Slaminka22
] for a historical account of the proof of Brouwer’s result.
$\tilde{U}$
, called sheets. We shall need the following celebrated result of Brouwer. Brouwer’s theorem with its subsequent generalisations is much stronger, but we shall only need the weaker version stated below. The reader is referred to [
Reference Slaminka22
] for a historical account of the proof of Brouwer’s result.
Theorem 2·1 (Brouwer Translation Theorem). [
Reference Brouwer7
] Let
![]() $h \,:\, \mathbb{R}^2 \to \mathbb{R}^2$
be an orientation preserving planar homeomorphism. If there exists an
$h \,:\, \mathbb{R}^2 \to \mathbb{R}^2$
be an orientation preserving planar homeomorphism. If there exists an
![]() $x\in\mathbb{R}^2$
such that
$x\in\mathbb{R}^2$
such that
![]() $\mathcal{O}(x)$
is bounded, then there exists a fixed point
$\mathcal{O}(x)$
is bounded, then there exists a fixed point
![]() $p\in\mathbb{R}^2$
of h.
$p\in\mathbb{R}^2$
of h.
Now we are ready to prove Theorem 1·1.
Proof (of Theorem 1·1). Let
![]() $\mathcal{O}(x)$
be a bounded orbit and
$\mathcal{O}(x)$
be a bounded orbit and
![]() $p\in\mathrm{Fix}(h)$
. If
$p\in\mathrm{Fix}(h)$
. If
![]() $p\in\mathrm{cl}(\mathcal{O}(x))\cap \mathrm{Fix}(h)$
then
$p\in\mathrm{cl}(\mathcal{O}(x))\cap \mathrm{Fix}(h)$
then
![]() $\mathcal{O}(x)$
and p are linked, and so from now on we shall assume that
$\mathcal{O}(x)$
and p are linked, and so from now on we shall assume that
![]() $\mathrm{cl}(\mathcal{O}(x))\cap \mathrm{Fix}(h)=\emptyset$
.
$\mathrm{cl}(\mathcal{O}(x))\cap \mathrm{Fix}(h)=\emptyset$
.
Standing Assumption:
![]() $\mathrm{cl}(\mathcal{O}(x))\cap \mathrm{Fix}(h)=\emptyset$
.
$\mathrm{cl}(\mathcal{O}(x))\cap \mathrm{Fix}(h)=\emptyset$
.
We start with the case when
![]() $K=\mathrm{cl}(\mathcal{O}(x))$
does not separate
$K=\mathrm{cl}(\mathcal{O}(x))$
does not separate
![]() $\mathbb{R}^2$
, as the case when K separates is easier.
$\mathbb{R}^2$
, as the case when K separates is easier.
Case I:
![]() $\mathrm{cl}(\mathcal{O}(x))$
does not separate
$\mathrm{cl}(\mathcal{O}(x))$
does not separate
![]() $\mathbb{R}^2$
.
$\mathbb{R}^2$
.
Refer to Figure 1. By contradiction, suppose that no point in
![]() $\mathrm{Fix}(h)$
is linked to
$\mathrm{Fix}(h)$
is linked to
![]() $\mathcal{O}(x)$
. Let U be the component of
$\mathcal{O}(x)$
. Let U be the component of
![]() $\mathbb{R}^2\setminus \mathrm{Fix}(h)$
that contains x. Recall that
$\mathbb{R}^2\setminus \mathrm{Fix}(h)$
that contains x. Recall that
![]() $h(U)=U$
by [
Reference Brown and Kister6
], and so
$h(U)=U$
by [
Reference Brown and Kister6
], and so
![]() $K\subset U$
. Note that U cannot be simply connected, as otherwise we obtain a contradiction with Brouwer Translation Theorem, since U is then homeomorphic to
$K\subset U$
. Note that U cannot be simply connected, as otherwise we obtain a contradiction with Brouwer Translation Theorem, since U is then homeomorphic to
![]() $\mathbb{R}^2$
and contains a bounded orbit, but no fixed point. Let
$\mathbb{R}^2$
and contains a bounded orbit, but no fixed point. Let
![]() $x_n=h^n(x)$
for each
$x_n=h^n(x)$
for each
![]() $\mathbb{N}$
. Let
$\mathbb{N}$
. Let
![]() $(\tilde{U},\tau)$
be the universal cover of U. Note that
$(\tilde{U},\tau)$
be the universal cover of U. Note that
![]() $\tilde{U}$
is homeomorphic to
$\tilde{U}$
is homeomorphic to
![]() $\mathbb{R}^2$
and, since K is contained in a disk disjoint from
$\mathbb{R}^2$
and, since K is contained in a disk disjoint from
![]() $\mathrm{Fix}(h)$
, K lifts to pairwise disjoint homeomorphic copies of itself (sheets) in
$\mathrm{Fix}(h)$
, K lifts to pairwise disjoint homeomorphic copies of itself (sheets) in
![]() $\tilde U$
, each of which maps homeomorphically onto K by
$\tilde U$
, each of which maps homeomorphically onto K by
![]() $\tau$
. Let
$\tau$
. Let
![]() $\tilde K$
be one such a sheet. We have
$\tilde K$
be one such a sheet. We have
![]() $\tau(\tilde{K})=K$
. Let
$\tau(\tilde{K})=K$
. Let
![]() $\tilde{x}=\tau^{-1}(x)\cap \tilde{K}$
and
$\tilde{x}=\tau^{-1}(x)\cap \tilde{K}$
and
![]() $\tilde{x}_1=\tau^{-1}(x_1)\cap \tilde{K}$
. The homeomorphism h lifts to a unique homeomorphism
$\tilde{x}_1=\tau^{-1}(x_1)\cap \tilde{K}$
. The homeomorphism h lifts to a unique homeomorphism
![]() $\tilde h$
such that
$\tilde h$
such that
![]() $\tilde{h}(\tilde{x})=\tilde x_1$
.
$\tilde{h}(\tilde{x})=\tilde x_1$
.
Claim 2·2.
![]() $\tilde{h}^n(\tilde{x})\in\tilde{K}$
for every
$\tilde{h}^n(\tilde{x})\in\tilde{K}$
for every
![]() $n\in\mathbb{N}$
.
$n\in\mathbb{N}$
.
Proof (of Claim 2·2). By contradiction, suppose that there exists an N such that
![]() $\tilde{h}^N(\tilde{x})\notin\tilde{K}$
.
$\tilde{h}^N(\tilde{x})\notin\tilde{K}$
.

Fig. 1. Proof of Theorem 1·1, Case I: The component U of
![]() $\mathbb{R}^2\setminus \mathrm{Fix}(h)$
containing
$\mathbb{R}^2\setminus \mathrm{Fix}(h)$
containing
![]() $\mathrm{cl}(\mathcal{O}(x))$
and the covering spaces
$\mathrm{cl}(\mathcal{O}(x))$
and the covering spaces
![]() $\tilde{U}$
and
$\tilde{U}$
and
![]() $\bar U$
.
$\bar U$
.
Without loss of generality we assume that
![]() $N=2$
. Let
$N=2$
. Let
![]() $\tilde{x}^{\prime}_2=\tau^{-1}(x_2)\cap \tilde K$
and
$\tilde{x}^{\prime}_2=\tau^{-1}(x_2)\cap \tilde K$
and
![]() $\tilde x_2=\tilde h(\tilde x_1)$
. We have
$\tilde x_2=\tilde h(\tilde x_1)$
. We have
![]() $\tilde x_2\in \tilde h(\tilde K)\neq \tilde K$
.
$\tilde x_2\in \tilde h(\tilde K)\neq \tilde K$
.
Let
![]() $\sigma\,:\,\tilde{U}\to\tilde{U}$
be the deck transformation such that
$\sigma\,:\,\tilde{U}\to\tilde{U}$
be the deck transformation such that
![]() $\sigma(\tilde x^{\prime}_2)=\tilde x_2$
. The deck transformation group is isomorphic to the fundamental group
$\sigma(\tilde x^{\prime}_2)=\tilde x_2$
. The deck transformation group is isomorphic to the fundamental group
![]() $\pi_1(U)$
of U, and one sees
$\pi_1(U)$
of U, and one sees
![]() $\sigma$
as an element
$\sigma$
as an element
![]() $\alpha$
of
$\alpha$
of
![]() $\pi_1(U)$
. There exists a point
$\pi_1(U)$
. There exists a point
![]() $p\in\mathrm{Fix}(h)$
, such that
$p\in\mathrm{Fix}(h)$
, such that
![]() $\alpha$
is a nontrivial loop in the surface
$\alpha$
is a nontrivial loop in the surface
![]() $W=\mathbb{R}^2\setminus \{p\}$
. Let
$W=\mathbb{R}^2\setminus \{p\}$
. Let
![]() $(\bar W, \kappa)$
be an infinite cyclic covering space of W. Then
$(\bar W, \kappa)$
be an infinite cyclic covering space of W. Then
![]() $(\tilde{U},\tau)$
is also a universal covering space of
$(\tilde{U},\tau)$
is also a universal covering space of
![]() $\bar U$
, the component of
$\bar U$
, the component of
![]() $\bar W\setminus \kappa^{-1}(\mathrm{Fix}(h)\setminus\{p\})$
that contains
$\bar W\setminus \kappa^{-1}(\mathrm{Fix}(h)\setminus\{p\})$
that contains
![]() $\kappa^{-1}(K)$
, and so there exists a covering map
$\kappa^{-1}(K)$
, and so there exists a covering map
![]() $\phi\,:\,\tilde U\to\bar U$
such that
$\phi\,:\,\tilde U\to\bar U$
such that
![]() $\tau=\kappa|_{\bar U}\circ\phi$
. Let
$\tau=\kappa|_{\bar U}\circ\phi$
. Let
![]() $\bar x=\phi(\tilde x), \bar x_1=\phi(\tilde x_1),\bar x_2=\phi(\tilde x_2)$
and
$\bar x=\phi(\tilde x), \bar x_1=\phi(\tilde x_1),\bar x_2=\phi(\tilde x_2)$
and
![]() $\bar x^{\prime}_2=\phi(\tilde x^{\prime}_2)$
. By the choice of
$\bar x^{\prime}_2=\phi(\tilde x^{\prime}_2)$
. By the choice of
![]() $\alpha$
we have that the element of the deck transformation group (with respect to
$\alpha$
we have that the element of the deck transformation group (with respect to
![]() $\bar U$
)
$\bar U$
)
![]() $\bar\sigma$
satisfying
$\bar\sigma$
satisfying
![]() $\bar \sigma\circ\phi=\phi \circ \sigma$
is nontrivial, and
$\bar \sigma\circ\phi=\phi \circ \sigma$
is nontrivial, and
![]() $\bar \sigma (\bar x^{\prime}_2)=\bar x_2$
, so
$\bar \sigma (\bar x^{\prime}_2)=\bar x_2$
, so
![]() $\bar x_2\neq \bar x^{\prime}_2$
. Let L be an unlinking of
$\bar x_2\neq \bar x^{\prime}_2$
. Let L be an unlinking of
![]() $\mathrm{cl}(\mathcal{O}(x))$
and
$\mathrm{cl}(\mathcal{O}(x))$
and
![]() $\{p\}$
. Set
$\{p\}$
. Set
![]() $\bar K=\phi(\tilde{K})$
, and let
$\bar K=\phi(\tilde{K})$
, and let
![]() $\bar L$
be a sheet over L that bounds a disk containing
$\bar L$
be a sheet over L that bounds a disk containing
![]() $\bar K$
, and
$\bar K$
, and
![]() $\bar h$
be the lift of h to
$\bar h$
be the lift of h to
![]() $\bar W$
given by
$\bar W$
given by
![]() $\bar h(\bar x)=\bar x_1$
. We have
$\bar h(\bar x)=\bar x_1$
. We have
![]() $\phi\circ \tilde h=(\bar h|\bar U)\circ\phi$
, and
$\phi\circ \tilde h=(\bar h|\bar U)\circ\phi$
, and
![]() $\bar h(\bar x_1)=\bar x_2$
.
$\bar h(\bar x_1)=\bar x_2$
.
Consider an isotopy
![]() $\{i_t\,:\,\mathbb{S}^1\rightarrow \mathbb{R}^2\setminus\left(\mathrm{cl}(\mathcal{O}(x))\cup\{p\}\right)\,:\,0\leq t\leq 1\}$
from
$\{i_t\,:\,\mathbb{S}^1\rightarrow \mathbb{R}^2\setminus\left(\mathrm{cl}(\mathcal{O}(x))\cup\{p\}\right)\,:\,0\leq t\leq 1\}$
from
![]() $i_0(\mathbb{S}^1)=L$
to
$i_0(\mathbb{S}^1)=L$
to
![]() $i_1(\mathbb{S}^1)=h(L)$
. By isotopy lifting property, this isotopy lifts to an isotopy
$i_1(\mathbb{S}^1)=h(L)$
. By isotopy lifting property, this isotopy lifts to an isotopy
![]() $\tilde{i}_t\,:\,\mathbb{S}^1\to\bar W\setminus\kappa^{-1}(\mathrm{cl}(\mathcal{O}(x)))$
taking
$\tilde{i}_t\,:\,\mathbb{S}^1\to\bar W\setminus\kappa^{-1}(\mathrm{cl}(\mathcal{O}(x)))$
taking
![]() $\bar{L}$
to
$\bar{L}$
to
![]() $\bar{h}(\bar{L})$
, both of which are loops in
$\bar{h}(\bar{L})$
, both of which are loops in
![]() $ {} {}\bar W$
(since L and h(L) are inessential in
$ {} {}\bar W$
(since L and h(L) are inessential in
![]() $\mathbb{R}^2\setminus\{p\}$
). This leads to a contradiction, since
$\mathbb{R}^2\setminus\{p\}$
). This leads to a contradiction, since
![]() $\bar{L}$
bounds a disk containing
$\bar{L}$
bounds a disk containing
![]() $\bar{x}_2$
, but
$\bar{x}_2$
, but
![]() $\tilde{h}(\bar{L})$
does not, so
$\tilde{h}(\bar{L})$
does not, so
![]() $\tilde{i}_t$
cannot take
$\tilde{i}_t$
cannot take
![]() $\bar{L}$
to
$\bar{L}$
to
![]() $\bar{h}(\bar{L})$
in
$\bar{h}(\bar{L})$
in
![]() $\bar W\setminus\kappa^{-1}(\mathrm{cl}(\mathcal{O}(x)))$
. This completes the proof of Claim 2·2.
$\bar W\setminus\kappa^{-1}(\mathrm{cl}(\mathcal{O}(x)))$
. This completes the proof of Claim 2·2.
To conclude the proof of Case I it is now enough to observe that
![]() $\tilde{h}$
is an orientation preserving homeomorphism of the plane
$\tilde{h}$
is an orientation preserving homeomorphism of the plane
![]() $\tilde{U}$
, with a compact invariant set
$\tilde{U}$
, with a compact invariant set
![]() $\tilde K$
, but no fixed points, contradicting Brouwer Translation Theorem.
$\tilde K$
, but no fixed points, contradicting Brouwer Translation Theorem.
Case II:
![]() $\mathrm{cl}(\mathcal{O}(x))$
separates
$\mathrm{cl}(\mathcal{O}(x))$
separates
![]() $\mathbb{R}^2$
.
$\mathbb{R}^2$
.
If no bounded component V of
![]() $\mathbb{R}^2\setminus\mathrm{cl}(\mathcal{O}(x))$
contains a fixed point then we add all such components to
$\mathbb{R}^2\setminus\mathrm{cl}(\mathcal{O}(x))$
contains a fixed point then we add all such components to
![]() $\mathrm{cl}(\mathcal{O}(x))$
and we are back to Case I.
$\mathrm{cl}(\mathcal{O}(x))$
and we are back to Case I.
Otherwise, there exists a bounded component
![]() $V_o$
of
$V_o$
of
![]() $\mathbb{R}^2\setminus\mathrm{cl}(\mathcal{O}(x))$
such that
$\mathbb{R}^2\setminus\mathrm{cl}(\mathcal{O}(x))$
such that
![]() $h(V_o)= V_o$
and
$h(V_o)= V_o$
and
![]() $V_o$
contains a fixed point p
′ of h. But since
$V_o$
contains a fixed point p
′ of h. But since
![]() $\partial V_o$
separates the plane into at least two components, one of which contains p
′, and none of which contains
$\partial V_o$
separates the plane into at least two components, one of which contains p
′, and none of which contains
![]() $\mathrm{cl}(\mathcal{O}(x))$
, there does not exist a disk
$\mathrm{cl}(\mathcal{O}(x))$
, there does not exist a disk
![]() $D_1$
such that
$D_1$
such that
![]() $\mathrm{cl}(\mathcal{O}(x))\subset \mathrm{int}(D_1)$
and
$\mathrm{cl}(\mathcal{O}(x))\subset \mathrm{int}(D_1)$
and
![]() $p^{\prime}\notin D_1$
. Consequently there is no unlinking of
$p^{\prime}\notin D_1$
. Consequently there is no unlinking of
![]() $\mathrm{cl}(\mathcal{O}(x))$
and p
′, and these two orbits must be linked. This concludes the proof of Case II.
$\mathrm{cl}(\mathcal{O}(x))$
and p
′, and these two orbits must be linked. This concludes the proof of Case II.
The proof of Theorem 1·1 is complete.
Remark 2·3. The proof of Theorem 1·1 remains valid if the full orbit
![]() $\mathcal{O}(x)$
is replaced with one of the half orbits
$\mathcal{O}(x)$
is replaced with one of the half orbits
![]() $\mathcal{O}^+(x)=\{h^n(x)\,:\,n\in\mathbb{N}\}$
or
$\mathcal{O}^+(x)=\{h^n(x)\,:\,n\in\mathbb{N}\}$
or
![]() $\mathcal{O}^-(x)=\{h^{-n}(x)\,:\,n\in\mathbb{N}\}$
.
$\mathcal{O}^-(x)=\{h^{-n}(x)\,:\,n\in\mathbb{N}\}$
.
3. Final remarks
In 1988 J. Franks defined what seems to be a deeper form of linking, for which one requires from a periodic orbit to have a non-zero rotation number around a fixed point. Franks asked whether every periodic orbit of an orientation preserving homeomorphism is linked in that sense to a fixed point [
Reference Boyland and Franks3
]. This difficult open problem was resolved in the affirmative by P. Le Calvez in 2006 [
Reference Le Calvez17
]. It seems that Le Calvez’s result cannot be extended to bounded orbits. A result that seems related to both forms of linking is proven in [
Reference Graff and Ruiz-Herrera12
], where a way of locating fixed points in proximity of recurrent orbits is given, by the means of topological hulls of unions of arcs, connecting a finite number of points of an
![]() $\epsilon$
-periodic orbit; see also [
Reference Kucharski16
] and [
Reference Ostrovski20
]. Sufficient conditions for the nonremovability of collections of periodic points under isotopy relative to a general compact invariant set can be found in [
Reference Boyland and Hall4
].
$\epsilon$
-periodic orbit; see also [
Reference Kucharski16
] and [
Reference Ostrovski20
]. Sufficient conditions for the nonremovability of collections of periodic points under isotopy relative to a general compact invariant set can be found in [
Reference Boyland and Hall4
].
Acknowledgments
I am grateful to Toby Hall for comments that helped to improve the paper, and an anonymous referee who pointed out a necessity to revise the initial proof of the main result. This work was supported in part by the National Science Centre, Poland (NCN), grant no. 2019/34/E/ST1/00237.