Published online by Cambridge University Press: 15 June 2009
Since the development of the calculus of variations there has been interest in finding critical points of functionals. This was intensified by the fact that for many equations arising in practice, the solutions are critical points. In searching for critical points, there is a distinct advantage if the functional G is semibounded. In this case one can find a Palais–Smale (PS) sequence or even a Cerami sequence
or even a Cerami sequence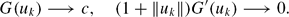 These sequences produce critical points if they have convergent subsequences. However, there is no clear method of finding critical points of functionals which are not semibounded. Linking subsets do provide such a method. They can produce a PS sequence provided they separate the functional. In the present paper we show that there are pairs of subsets that can produce Cerami-like sequences even though they do not separate the functional. All that is required is that the functional be bounded from above on one of the sets and bounded from below on the other, with no relationship needed between the bounds. This provides a distinct advantage in applications. We apply the method to several situations.
These sequences produce critical points if they have convergent subsequences. However, there is no clear method of finding critical points of functionals which are not semibounded. Linking subsets do provide such a method. They can produce a PS sequence provided they separate the functional. In the present paper we show that there are pairs of subsets that can produce Cerami-like sequences even though they do not separate the functional. All that is required is that the functional be bounded from above on one of the sets and bounded from below on the other, with no relationship needed between the bounds. This provides a distinct advantage in applications. We apply the method to several situations.