Locally compact groups with closed subgroups open and p-adic
Published online by Cambridge University Press: 24 October 2008
Extract
An open subgroup U of a topological group G is always closed, since U is the complement of the open set 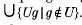 . An arbitrary closed subgroup C of G is almost never open, unless G belongs to a small family of exceptional groups. In fact, if G is a locally compact abelian group in which every non-trivial subgroup is open, then G is the additive group δp of p-adic integers or the additive group Ωp of p-adic rationale (cf. Robertson and Schreiber[5[, proposition 7). The fact that δp has interesting properties as a topological group has many roots. One is that its character group is the Prüfer group ℤp∞, which makes it unique inside the category of compact abelian groups. But even within the bigger class of not necessarily abelian compact groups the p-adic group δp is distinguished: it is the only one all of whose non-trivial subgroups are isomorphic (cf. Morris and Oates-Williams[2[), and it is also the only one all of whose non-trivial closed subgroups have finite index (cf. Morris, Oates-Williams and Thompson [3[).
. An arbitrary closed subgroup C of G is almost never open, unless G belongs to a small family of exceptional groups. In fact, if G is a locally compact abelian group in which every non-trivial subgroup is open, then G is the additive group δp of p-adic integers or the additive group Ωp of p-adic rationale (cf. Robertson and Schreiber[5[, proposition 7). The fact that δp has interesting properties as a topological group has many roots. One is that its character group is the Prüfer group ℤp∞, which makes it unique inside the category of compact abelian groups. But even within the bigger class of not necessarily abelian compact groups the p-adic group δp is distinguished: it is the only one all of whose non-trivial subgroups are isomorphic (cf. Morris and Oates-Williams[2[), and it is also the only one all of whose non-trivial closed subgroups have finite index (cf. Morris, Oates-Williams and Thompson [3[).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 118 , Issue 2 , September 1995 , pp. 303 - 313
- Copyright
- Copyright © Cambridge Philosophical Society 1995
References
REFERENCES
- 3
- Cited by


