Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Buchdahl, N. P.
Kwasik, S?awomir
and
Schultz, Reinhard
1990.
One fixed point actions on low-dimensional spheres.
Inventiones Mathematicae,
Vol. 102,
Issue. 1,
p.
633.
Kwasik, Slawomir
and
Schultz, Reinhard
1992.
Icosahedral group actions on R3.
Inventiones Mathematicae,
Vol. 108,
Issue. 1,
p.
385.
Liu, Ximin
and
Nakamura, Nobuhiro
2008.
Nonsmoothable group actions on elliptic surfaces.
Topology and its Applications,
Vol. 155,
Issue. 9,
p.
946.
Kiyono, Kazuhiko
2011.
Nonsmoothable group actions on spin 4–manifolds.
Algebraic & Geometric Topology,
Vol. 11,
Issue. 3,
p.
1345.
Galaz-Garcia, Fernando
and
Guijarro, Luis
2015.
On Three-Dimensional Alexandrov Spaces.
International Mathematics Research Notices,
Vol. 2015,
Issue. 14,
p.
5560.
Khan, Qayum
2018.
Countable approximation of topological G-manifolds: Compact Lie groups G.
Topology and its Applications,
Vol. 235,
Issue. ,
p.
14.
LANGE, CHRISTIAN
2018.
Equivariant smoothing of piecewise linear manifolds.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 164,
Issue. 2,
p.
369.
Turiel, F. J.
and
Viruel, A.
2020.
Finite groups of diffeomorphisms are topologically determined by a vector field.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 3,
Grillet, Lucien
2023.
Smoothing finite‐order bilipschitz homeomorphisms of 3‐manifolds.
Journal of Topology,
Vol. 16,
Issue. 3,
p.
1093.

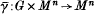 and an equivariant homeomorphism
and an equivariant homeomorphism 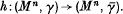 It is well known that for
It is well known that for 