Published online by Cambridge University Press: 24 October 2008
The Landau–Kolmogorov inequality
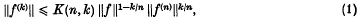
where ‖.‖ is the ‘sup’ norm, is well known and has many interesting applications and generalizations (see [1, 4–7, 13, 16]). Its study was initiated by Landau[10] and Hadamard [8] (the case n = 2). Kolmogorov [9] succeeded in finding in explicit form the best possible constants K(n, k) = Cn, k in (1) for functions on the whole real line R. The best constants 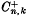 for the half line R+ are not known in explicit form except for n = 2, 3, 4, but an algorithm exists for their computation (Schoenberg and Cavaretta [15]).
for the half line R+ are not known in explicit form except for n = 2, 3, 4, but an algorithm exists for their computation (Schoenberg and Cavaretta [15]).