Metric Diophantine approximation with two restricted variables I. Two square-free integers, or integers in arithmetic progressions
Published online by Cambridge University Press: 24 October 2008
Extract
In this paper, together with [7] and [8], we shall be concerned with estimating the number of solutions of the inequality
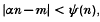
for almost all α (in the sense of Lebesgue measure on Iℝ), where 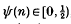 , and both m and n are restricted to sets of number-theoretic interest. Our aim is to prove results analogous to the following theorem (an improvement given in [2] of an earlier result of Khintchine [10]) and its quantitative developments (for example, see [11, 12,6]):
, and both m and n are restricted to sets of number-theoretic interest. Our aim is to prove results analogous to the following theorem (an improvement given in [2] of an earlier result of Khintchine [10]) and its quantitative developments (for example, see [11, 12,6]):
Let ψ(n) be a non-increasing positive function of a positive integer variable n. Then the inequality (1·1) has infinitely many, or only finitely many, solutions in integers to, n(n > 0) for almost all real α, according to whether the sum
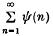
diverges, or converges, respectively.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 103 , Issue 2 , March 1988 , pp. 197 - 206
- Copyright
- Copyright © Cambridge Philosophical Society 1988
References
REFERENCES
- 9
- Cited by


