Article contents
Mock theta functions and weakly holomorphic modular forms modulo 2 and 3
Published online by Cambridge University Press: 04 December 2014
Abstract
We prove that the coefficients of the mock theta functions
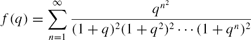 \begin{eqnarray*}
f(q) = \sum_{n=1}^{\infty} \frac{ q^{n^2}}{(1+q)^2 (1+q^2)^2 \cdots (1+q^n)^2 }
\end{eqnarray*}
\begin{eqnarray*}
f(q) = \sum_{n=1}^{\infty} \frac{ q^{n^2}}{(1+q)^2 (1+q^2)^2 \cdots (1+q^n)^2 }
\end{eqnarray*}
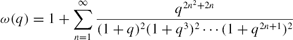 \begin{eqnarray*}
\omega(q)=1+\sum_{n=1}^\infty \frac{q^{2n^2+2n}}{(1+q)^2(1+q^3)^2\cdots (1+q^{2n+1})^2}
\end{eqnarray*}
\begin{eqnarray*}
\omega(q)=1+\sum_{n=1}^\infty \frac{q^{2n^2+2n}}{(1+q)^2(1+q^3)^2\cdots (1+q^{2n+1})^2}
\end{eqnarray*}
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 158 , Issue 1 , January 2015 , pp. 111 - 129
- Copyright
- Copyright © Cambridge Philosophical Society 2014
References
REFERENCES
- 4
- Cited by


