Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Stewartson, K.
1957.
The dispersion of a current on the surface of a highly conducting fluid.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 53,
Issue. 3,
p.
774.
Stewartson, K.
1960.
On the motion of a non-conducting body through a perfectly conducting fluid.
Journal of Fluid Mechanics,
Vol. 8,
Issue. 01,
p.
82.
Ludford, G. S. S.
1960.
Inviscid Flow past a Body at Low Magnetic Reynolds Number.
Reviews of Modern Physics,
Vol. 32,
Issue. 4,
p.
1000.
Stewartson, K.
1960.
Motion of Bodies through Conducting Fluids.
Reviews of Modern Physics,
Vol. 32,
Issue. 4,
p.
855.
Hasimoto, Hidenori
1960.
Magnetohydrodynamic Wakes in a Viscous Conducting Fluid.
Reviews of Modern Physics,
Vol. 32,
Issue. 4,
p.
860.
Chopra, K. P.
1961.
Interactions of Rapidly Moving Bodies in Terrestrial Atmosphere.
Reviews of Modern Physics,
Vol. 33,
Issue. 2,
p.
153.
Ludford, G. S. S.
1961.
The effect of a very strong magnetic cross-field on steady motion through a slightly conducting fluid.
Journal of Fluid Mechanics,
Vol. 10,
Issue. 1,
p.
141.
Ludford, G. S. S.
1961.
The effect of a very strong magnetic cross-field on steady motion through a slightly conducting fluid: Three-dimensional case.
Archive for Rational Mechanics and Analysis,
Vol. 8,
Issue. 1,
p.
242.
Hide, Raymond
and
Roberts, Paul H.
1962.
Advances in Applied Mechanics Volume 7.
Vol. 7,
Issue. ,
p.
215.
Stewartson, Keith
1962.
Magneto-fluid dynamics of thin bodies in oblique fields (II).
Zeitschrift für angewandte Mathematik und Physik ZAMP,
Vol. 13,
Issue. 3,
p.
242.
LUDFORD, G. S. S.
and
SINGH, M. P.
1963.
HYDROMAGNETICS OF A SPHERICAL CONDUCTOR.
AIAA Journal,
Vol. 1,
Issue. 11,
p.
2660.
Ludford, G. S. S.
and
Singh, M. P.
1963.
On the motion of a sphere through a conducting fluid in the presence of a magnetic field.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 3,
p.
625.
LIEN, HWACHII
and
YEH, HSUAN
1963.
APPROXIMATE METHOD FOR CALCULATING MAGNETOHYDRODYNAMIC BOUNDARY LAYER AND HEAT TRANSFER OF A SLIGHTLY CONDUCTING FLUID PAST A CYLINDRICALBODY.
Ludford, G. S. S.
and
Singh, M. P.
1963.
The motion of a non-conducting sphere through a conducting fluid in a magnetic cross-field.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 3,
p.
615.
Clauser, Francis H.
1963.
Concept of Field Modes and the Behavior of the Magnetohydrodynamic Field.
The Physics of Fluids,
Vol. 6,
Issue. 2,
p.
231.
Ludford, G. S. S.
and
Singh, M. P.
1964.
The hydromagnetics of an ellipsoid moving in a cross-field.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 60,
Issue. 2,
p.
341.
1964.
Magnetohydrodynamics with Hydrodynamics.
p.
174.
Sears, W.R.
and
Resler, E.L.
1964.
Advances in Applied Mechanics Volume 8.
Vol. 8,
Issue. ,
p.
1.
Ness, Norman F.
1965.
The magnetohydrodynamic wake of the Moon.
Journal of Geophysical Research,
Vol. 70,
Issue. 3,
p.
517.
Parbhakar, Kanwal J.
and
Uberoi, Mahinder S.
1969.
Magnetohydrodynamic Flow Past Axisymmetric Bodies with Aligned Magnetic Field.
The Physics of Fluids,
Vol. 12,
Issue. 10,
p.
2083.
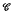 of fluid whose generators are parallel to the direction of the field moves with the sphere as if solid. The streamlines outside
of fluid whose generators are parallel to the direction of the field moves with the sphere as if solid. The streamlines outside 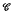 are straight lines if the sphere moves in the direction of the field but have to execute sharp turns if it moves at right angles to the field. The motion to be expected in practice is discussed using an analogy.
are straight lines if the sphere moves in the direction of the field but have to execute sharp turns if it moves at right angles to the field. The motion to be expected in practice is discussed using an analogy.