Published online by Cambridge University Press: 01 May 2008
This paper investigates the natural problem of performing the multifractal analysis of heterogeneous sums of Dirac masses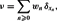 where (xn)n≥0 is a sequence of points in [0, 1]d and (wn)n≥0 is a positive sequence of weights such that Σn≥0wn < ∞. We consider the case where the points xn are roughly uniformly distributed in [0, 1]d, and the weights wn depend on a random self-similar measure μ, a parameter ρ ∈ (0, 1], and a sequence of positive radii (λn)n≥1 converging to 0 in the following way
where (xn)n≥0 is a sequence of points in [0, 1]d and (wn)n≥0 is a positive sequence of weights such that Σn≥0wn < ∞. We consider the case where the points xn are roughly uniformly distributed in [0, 1]d, and the weights wn depend on a random self-similar measure μ, a parameter ρ ∈ (0, 1], and a sequence of positive radii (λn)n≥1 converging to 0 in the following way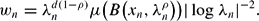 The measure ν has a rich multiscale structure. The computation of its multifractal spectrum is related to heterogeneous ubiquity properties of the system {(xn,λn)n with respect to μ.
The measure ν has a rich multiscale structure. The computation of its multifractal spectrum is related to heterogeneous ubiquity properties of the system {(xn,λn)n with respect to μ.