Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T03:28:06.355Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicatively badly approximable matrices up to logarithmic factors

Part of: Geometry of numbers Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  17 May 2021

REYNOLD FREGOLI
REYNOLD FREGOLI*
Affiliation:
Department of Mathematics, Bedford Building, Royal Holloway University of London, Egham Hill, TW20 0EX UK e-mail: Reynold.Fregoli.2017@live.rhul.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 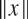\[||x||\] denote the distance from 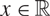\[x \in \mathbb{R}\] to the nearest integer. In this paper, we prove a new existence and density result for matrices 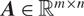\[A \in {\mathbb{R}^{m \times n}}\] satisfying the inequality

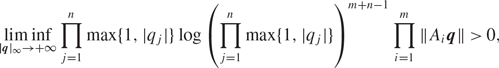\[\mathop {\lim \inf }\limits_{|q{|_\infty } \to + \infty } \prod\limits_{j = 1}^n {\max } \{ 1,|{q_j}|\} \log {\left( {\prod\limits_{j = 1}^n {\max } \{ 1,|{q_j}|\} } \right)^{m + n - 1}}\prod\limits_{i = 1}^m {{A_i}q} > 0,\]

where q ranges in 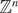\[{\mathbb{Z}^n}\] and Ai denote the rows of the matrix A. This result extends previous work of Moshchevitin both to arbitrary dimension and to the inhomogeneous setting. The estimates needed to apply Moshchevitin’s method to the case m > 2 are not currently available. We therefore develop a substantially different method, based on Cantor-like set constructions of Badziahin and Velani. Matrices with the above property also appear to have very small sums of reciprocals of fractional parts. This fact helps us to shed light on a question raised by Lê and Vaaler on such sums, thereby proving some new estimates in higher dimension.

MSC classification

Primary: 11J13: Simultaneous homogeneous approximation, linear forms 11J20: Inhomogeneous linear forms 11J83: Metric theory 11H46: Products of linear forms
Secondary: 11H16: Nonconvex bodies
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 3 , May 2022 , pp. 685 - 703
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badziahin, D.. On multiplicatively badly approximable numbers. Mathematika, 59 (No. 1) (2013), 31–55.CrossRefGoogle Scholar
Badziahin, D. and Velani, S.. Multiplicatively badly approximable numbers and generalised Cantor sets. Adv. in Math., 228 (No. 5) (2011), 2766–2796.CrossRefGoogle Scholar
Beresnevich, V., Haynes, A. and Velani, S.. Memoirs of the American Mathematical Society 263 (No. 1276) (2020).CrossRefGoogle Scholar
Beresnevich, V. and Velani, S.. Classical metric Diophantine approximation revisited: the Khintchine-Groshev Theorem. Int. Math. Res. Not. (No. 1) (2010), 69–86.Google Scholar
Bugeaud, Y.. Multiplicative Diophantine approximation. Dynamical systems and Diophantine approximation. Proc. Conf. Inst. H. Poincaré (Société Mathématique de France, Paris) (2009), 105–125.Google Scholar
Bugeaud, Y. and Moshchevitin, N.. Badly approximable numbers and Littlewood-type problems. Math. Proc. Cambridge Phil. Soc. 150 (No. 2) (2011), 215–226.CrossRefGoogle Scholar
Einsiedler, M., Katok, A. and Lindenstrauss, E., Invariant measures and the set of exceptions to Littlewood’s conjecture, Ann. of Math. 164 (2006), 513–560.CrossRefGoogle Scholar
Fregoli, R.. Sums of reciprocals of fractional parts. Int. J. Number Theory. 15 (No. 4) 2019, 789–797.CrossRefGoogle Scholar
Fregoli, R.. On a counting theorem for weakly admissible lattices. Int. Mat. Res. Not. rnaa102 (2020).CrossRefGoogle Scholar
Gallagher, P.. Metric simultaneous Diophantine approximation. J. London Math. Soc. 37 (No. 1) (1962), 387–390.CrossRefGoogle Scholar
Kruse, A. H.. Estimates of \[\sum\nolimits_{k = 1}^N {{k^{ - s}}{\mkern 1mu} < kx{ > ^{ - t}}} \]. Trans. Amer. Math. Soc. 110 (1964), 493–518.Google Scholar
Lê, T. H. and Vaaler, J. D.. Sums of products of fractional parts. Proc. London Math. Soc. 111 (No. 3) (2014), 561–590.Google Scholar
Moshchevitin, N.. Badly approximable numbers related to the Littlewood conjecture. arXiv:0810.0777 [math.NT] (2008).Google Scholar
Peck, L. G.. Simultaneous rational approximations to algebraic numbers. Bull. A.M.S. 67 (1961), 197–201.CrossRefGoogle Scholar
Pollington, A. and Velani, S.. On a problem in simultaneous Diophantine approximation: Littlewood’s conjecture. Acta Math. 66 (2000), 29–40.Google Scholar
Schmidt, W. M.. Badly approximable systems of linear forms. J. Number Theory. 1 (1969), 139–154.CrossRefGoogle Scholar
Sprindžuk, V. G.. Metric Theory of Diophantine Approximations (in Russian). (Nauka, 1977).Google Scholar