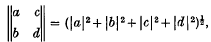Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kamiya, Shigeyasu
1991.
Notes on elements of ${\rm U}(1,n;{\bf C})$.
Hiroshima Mathematical Journal,
Vol. 21,
Issue. 1,
Wilker, J.B.
1993.
The quaternion formalism for Möbius groups in four or fewer dimensions.
Linear Algebra and its Applications,
Vol. 190,
Issue. ,
p.
99.
Beardone, Alan F.
2001.
Continued Fractions, Discrete Groups and Complex Dynamics.
Computational Methods and Function Theory,
Vol. 1,
Issue. 2,
p.
535.
Beardon, A.F.
and
Lorentzen, L.
2004.
Continued Fractions and Restrained Sequences of Möbius Maps.
Rocky Mountain Journal of Mathematics,
Vol. 34,
Issue. 2,


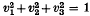 , and its Poincaré extension acts as an isometry of hyperbolic 3-space modelled in the ball
, and its Poincaré extension acts as an isometry of hyperbolic 3-space modelled in the ball 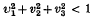 < 1. The size of this transformation can be measured by the matrix norm
< 1. The size of this transformation can be measured by the matrix norm