Published online by Cambridge University Press: 24 October 2008
P. M. Cohn has given a characterization of pseudovaluation on a field in (1). There he defines the notion of an integral element over a multiplicatively closed set and states that the association of the set A to the set A* of all elements that are integral over it is a closure operator. There is an error in the statement that A* = (A*)*. In this note we show, by an example, that A* and (A*)* are not equal in general. We also give an example to show that even for the special type of sets that Cohn needs, namely the gauge sets, this property fails to hold. However, since the other conditions for a closure operator (A ⊆ A* and A ⊆ B implies A* ⊆ B*) are satisfied, one obtains a Kuratowski closure operator by iterating *. If we denote by Ā the closure of A by iterating * then theorem 10·3, its corollary and theorem 10·4 in (1) that have a bearing on this error, are valid as stated with the same proof replacing only K* by 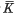 . Further theorem 13·3 is valid without modification since Cohn considers only a special class of pseudovaluations namely regular pseudo valuations for which K* =
. Further theorem 13·3 is valid without modification since Cohn considers only a special class of pseudovaluations namely regular pseudo valuations for which K* = 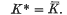 .
.