Note on a problem of Porte
Published online by Cambridge University Press: 24 October 2008
Extract
Porte (1), p. 117, conjectures that the positive implicational propositional calculus has no finite characteristic matrix. The proof of this conjecture is a straightforward modification of Gödel's proof (2) that the intuitionistic propositional calculus has no finite characteristic matrix (see e.g. Church(3), ex. 26.12). Writing (A ∨ B) for ((A ⊃ B) ⊃ B) and Xij for (pj ⊃ pi) (i, j = 1,2,…), we define, for n > l, the formula
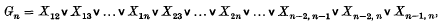
where the terms associate to the left. Since provable formulae take the value n for all systems of values of the variables in the matrix {1,…,n} where x ⊃ y is n when x ≤ y and y otherwise, whereas Gn takes the value n − 1 for the system of values pi = i (i = 1,…,n), it follows that Gn is not provable. On the other hand, since A ⊢ A ∨ B and B ⊢ A ∨ B, it is easily seen that 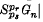 is provable whenever r ≠ s (r, s = 1,…,n). The result follows from these two remarks.
is provable whenever r ≠ s (r, s = 1,…,n). The result follows from these two remarks.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 1 , January 1968 , pp. 1
- Copyright
- Copyright © Cambridge Philosophical Society 1968
References
REFERENCES
- 1
- Cited by


