Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cusick, T. W.
1984.
Finding fundamental units in totally real fields.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 96,
Issue. 2,
p.
191.
Cusick, T. W.
and
Schoenfeld, Lowell
1987.
A table of fundamental pairs of units in totally real cubic fields.
Mathematics of Computation,
Vol. 48,
Issue. 177,
p.
147.
Hambleton, Samuel A.
and
Williams, Hugh C.
2018.
Cubic Fields with Geometry.
p.
277.


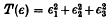 . Let ε be a unit for which T (ε) is least and let η be a unit, not a power of ε, for which T(η) is least. It was shown by Cusick[l] that ε,η form a pair of fundamental units under certain conditions. The purpose of the present note is to show that these conditions are unnecessary and that ε, η form a pair of fundamental units in all cases.
. Let ε be a unit for which T (ε) is least and let η be a unit, not a power of ε, for which T(η) is least. It was shown by Cusick[l] that ε,η form a pair of fundamental units under certain conditions. The purpose of the present note is to show that these conditions are unnecessary and that ε, η form a pair of fundamental units in all cases.