Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Marar, W.L.
Nuño-Ballesteros, J.J.
and
Peñafort-Sanchis, G.
2012.
Double point curves for corank 2 map germs from C2 to C3.
Topology and its Applications,
Vol. 159,
Issue. 2,
p.
526.
Némethi, András
and
Pintér, Gergő
2018.
The boundary of the Milnor fibre of certain non-isolated singularities.
Periodica Mathematica Hungarica,
Vol. 77,
Issue. 1,
p.
34.
Peñafort Sanchis, Guillermo
2020.
Reflection maps.
Mathematische Annalen,
Vol. 378,
Issue. 1-2,
p.
559.
Nuño‐Ballesteros, J. J.
and
Sanchis, G. Peñafort
2023.
Iterated multiple points I: Equations and pathologies.
Journal of the London Mathematical Society,
Vol. 107,
Issue. 1,
p.
213.
Giménez Conejero, R.
and
Nuño-Ballesteros, J. J.
2024.
A weak version of the Mond conjecture.
Collectanea Mathematica,
Vol. 75,
Issue. 3,
p.
753.


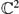 , 0) → (
, 0) → ( , 0). Examples and counter examples of such map germs are presented.
, 0). Examples and counter examples of such map germs are presented.