No CrossRef data available.
A note on the strong regularity of Nrlund means
Published online by Cambridge University Press: 24 October 2008
Extract
Let (pn), (qn) and (un) be sequences of real or complex numbers with
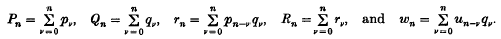
The sequence (sn) is strongly generalized Nrlund summable with index 0, to s, or s or snsN, p, Q if
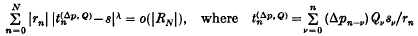
and pnv=pnvpnv1, with p10. Strong Nrlund summability N, p was first studied by Borweing and Cass (1), and its generalization N, p, Q by Thorp (6). We shall say that (sn) is strongly generalized convergent of index 0, to s, and write snsC, 0, Q if sns and 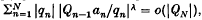 where sn=a0+a1++an. When qn all n, this definition reduces to strong convergence of index , introduced by Hyslop (4). If
where sn=a0+a1++an. When qn all n, this definition reduces to strong convergence of index , introduced by Hyslop (4). If  as n, the sequence (sn) is summable (
as n, the sequence (sn) is summable (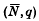 , q) to s sns(
, q) to s sns(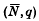 , q).
, q).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 2 , September 1983 , pp. 261 - 263
- Copyright
- Copyright © Cambridge Philosophical Society 1983


