I. Convergence of directed nets
Published online by Cambridge University Press: 24 October 2008
There is a close parallelism between the theories of convergence of directed nets and of filters, in which ‘subnet’ corresponds, in general, to ‘refinement’. With the standard definitions, however (1), pages 65 et seq., this correspondence is not exact, as there is no coarsest net converging to x0 of which all other nets with the same limit are subnets. (Suppose, for example, that a net X = {xj,: j ∈ J} in R1 has both the sequence-net S = {n−1; n = 1, 2,…} and the singleton-net {0} as subnets. Then (with an obvious notation), there exist
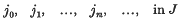
such that j0 ≥ jn for all n, while jn ≥ j0 for all n ≥ n0 say. But, given any j ∈ J, there exists n with jn ≥ j: it follows that jn ∈ j for all n ≥ n0 (independent of j); thus X cannot converge to 0. Even if nets with a last member are excluded, a similar result can be obtained by considering the net Y = {yθ; Θ an ordinal less than ω1}, where yθ = 0 for all Θ. If X has both Y and S as subnets we can show that (with a similar notation) there exists Θ0 such that Θ ≥ Θ0 implies jθ ≥ all jn, but also n0 such that n ≥ n0 implies 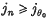 ; the rest is as before.) Moreover, the theory of convergence classes, (l), pages 73 et seq., contains a condition (Kelley's condition (c)) whose analogue need not be separately stated for filters. These differences can be removed by adopting a wider definition of subnet, a course which does not seem unnatural, inasmuch as the standard definition is already wider than the ‘obvious’ one, and our proposed definition is equivalent to the standard one in the special case of sequences.
; the rest is as before.) Moreover, the theory of convergence classes, (l), pages 73 et seq., contains a condition (Kelley's condition (c)) whose analogue need not be separately stated for filters. These differences can be removed by adopting a wider definition of subnet, a course which does not seem unnatural, inasmuch as the standard definition is already wider than the ‘obvious’ one, and our proposed definition is equivalent to the standard one in the special case of sequences.