Numbers badly approximate by fractions with prime denominator
Published online by Cambridge University Press: 24 October 2008
Extract
We write ‖x‖ to denote the least distance from x to an integer, and write p for a prime variable. Duffin and Schaeffer [l] showed that for almost all real α the inequality

has infinitely many solutions if and only if
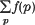
diverges. Thus f(x) = (x log log (10x))−1 is a suitable choice to obtain infinitely many solutions for almost all α. It has been shown [2] that for all real irrational α there are infinitely many solutions to (1) with f(p) = p−/13. We will show elsewhere that the exponent can be increased to 7/22. A very strong result on primes in arithmetic progressions (far stronger than anything within reach at the present time) would lead to an improvement on this result. On the other hand, it is very easy to find irrational a such that no convergent to its continued fraction expansion has prime denominator (for example (45– √10)/186 does not even have a square-free denominator in its continued fraction expansion, since the denominators are alternately divisible by 4 and 9).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 118 , Issue 1 , July 1995 , pp. 1 - 5
- Copyright
- Copyright © Cambridge Philosophical Society 1995
References
REFERENCES
- 4
- Cited by


