Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
James, Gordon D.
1980.
The decomposition of tensors over fields of prime characteristic.
Mathematische Zeitschrift,
Vol. 172,
Issue. 2,
p.
161.
Walker, Grant
1994.
Modular Schur functions.
Transactions of the American Mathematical Society,
Vol. 346,
Issue. 2,
p.
569.
Kleshchev, A. S.
1998.
Algebraic Groups and their Representations.
p.
103.
Chuang, Joseph
and
Tan, Kai Meng
1999.
On Young Modules of Defect 2 Blocks of Symmetric Group Algebras.
Journal of Algebra,
Vol. 221,
Issue. 2,
p.
651.
Tsushima, Yukio
2003.
On some SR(H)-blocks for the symmetric groups.
Journal of Algebra,
Vol. 270,
Issue. 1,
p.
281.
Lyle, Sinéad
2003.
Some reducible Specht modules.
Journal of Algebra,
Vol. 269,
Issue. 2,
p.
536.
Henke, Anne
2005.
On p-Kostka numbers and Young modules.
European Journal of Combinatorics,
Vol. 26,
Issue. 6,
p.
923.
Lyle, Sinéad
2007.
Some q-analogues of the Carter-Payne theorem.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2007,
Issue. 608,
NEUMANN, PETER M.
PRAEGER, CHERYL E.
and
SMITH, SIMON M.
2017.
SOME INFINITE PERMUTATION GROUPS AND RELATED FINITE LINEAR GROUPS.
Journal of the Australian Mathematical Society,
Vol. 102,
Issue. 1,
p.
136.
Craven, David A.
2019.
Representation Theory of Finite Groups: a Guidebook.
p.
167.
Mathas, Andrew
2022.
Gordon Douglas James, 1945–2020.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 6,
p.
2561.
Fayers, Matthew
and
Morotti, Lucia
2023.
On the irreducible spin representations of symmetric and alternating groups which remain irreducible in characteristic 3.
Representation Theory of the American Mathematical Society,
Vol. 27,
Issue. 22,
p.
778.
Gao, Zhao
and
Raicu, Claudiu
2024.
Cohomology of line bundles on the incidence correspondence.
Transactions of the American Mathematical Society, Series B,
Vol. 11,
Issue. 2,
p.
64.
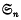 remain irreducible modulo a prime p?
remain irreducible modulo a prime p?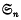 corresponding to the partition λ. Thus we are interested in the problem of whether or not Sλ is irreducible over a field of characteristic p.
corresponding to the partition λ. Thus we are interested in the problem of whether or not Sλ is irreducible over a field of characteristic p.

