Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T04:21:51.591Z Has data issue: false hasContentIssue false
  • English
  • Français

On a conjecture of Watson

Published online by Cambridge University Press:  24 October 2008

Madhu Raka
Madhu Raka
Affiliation:
Panjab University, Chandigarh-160014, India
Get access Rights & Permissions [Opens in a new window]

Extract

Let Qn be a real indefinite quadratic form in n variables x1, x2,…, xn, of determinant D ≠ 0 and of type (r, s), 0 < r < n, n = r + s. Let σ denote the signature of Qn so that σ = r − s. It is known (see e.g. Blaney(4)) that, given any real numbers c1 c2, …, cn, there exists a constant C depending upon n and σ only such that the inequality

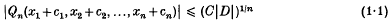
has a solution in integers x1, x2, …, xn. Let Cr, s denote the infimum of all such constants. Clearly Cr, s = Cs, r, so we need consider non-negative signatures only. For n = 2, C1, 1 = ¼ follows from a classical result of Minkowski on the product of two linear forms. When n = 3, Davenport (5) proved that C2, 1 = 27/100. For all n and σ = 0, Birch (3) proved that Cr, r = ¼. In 1962, Watson(18) determined the values of Cr, s for all n ≥ 21 and for all signatures σ. He proved that

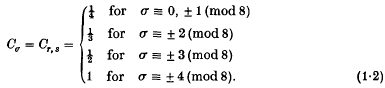
Watson also conjectured that (1·2) holds for all n ≥ 4. Dumir(6) proved Watson's conjecture for n = 4. For n = 5, it was proved by Hans-Gill and Madhu Raka(7, 8). The author (12) has proved the conjecture for σ = 1 and all n. In the preceding paper (13) we proved that C5, 1 = 1. In this paper we prove Watson's conjecture for σ = 2, 3 and 4.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 1 , July 1983 , pp. 9 - 22
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bambah, R. P., Dumir, V. C. and Hans-Gill, R. J.On a conjecture of Jackson on non-homogeneous quadratic forms. J. Number Theory (accepted).Google Scholar
(2)Barnes, E. S.The non-negative values of quadratic forms. Proc. Lond. Math. Soc. (3), 5 (1955), 185–196.CrossRefGoogle Scholar
(3)Birch, B. J.The inhomogeneous minimum of quadratic forms of signature zero. Acta Arith. 4 (1958), 85–98.CrossRefGoogle Scholar
(4)Blaney, H.Indefinite quadratic forms in n variables. Proc. Lond. Math. Soc. 23 (1948), 153–160.CrossRefGoogle Scholar
(5)Davenport, H.Non-homogeneous ternary quadratic forms. Acta Math. 80 (1948), 65–95.CrossRefGoogle Scholar
(6)Dumir, V. C.Inhomogeneous minimum of indefinite quaternary quadratic forms. Proc. Cambridge Philos. Soc. 63 (1967), 277–290.CrossRefGoogle Scholar
(7)Hans-Gill, R. J. and Madhu, Raka. Inhomogeneous minimum of 5-ary quadratic forms of type (3, 2) or (2, 3); a conjecture of Watson. Monatsh. Math. 88 (1979), 305–320.CrossRefGoogle Scholar
(8)Hans-Gill, R. J. and Madhu, Raka. Inhomogeneous minimum of indefinite quadratic forms in five variables of type (4, 1) or (1,4); a conjecture of Watson. Indian J. pure appl. Math. 11 (1) (1980), 75–91.Google Scholar
(9)Jackson, T. H.Small positive values of indefinite quadratic forms J. Lond. Math. Soc. (2), 1 (1969), 643–659.CrossRefGoogle Scholar
(10)Jackson, T. H.Gaps between the values of quadratic polynomials. J. Lond. Math. Soc. (2), 3 (1971), 47–58.CrossRefGoogle Scholar
(11)Korkine, A. and Zolotareff, G.Sur les formes quadratiques positives. Math. Ann. 11 (1877), 242–292.CrossRefGoogle Scholar
(12)Madhu, Raka. The inhomogeneous minimum of quadratic forms of signature ± 1. Math. Proc. Cambridge Philos. Soc. 89 (1981), 225–235.Google Scholar
(13)Madhu, Raka. Inhomogneous minimum of indefinite quadratic forms in six variables: a Conjecture of Watson. Math. Proc. Cambridge Philos. Soc. 94 (1983), 1–8.Google Scholar
(14)Oppenheim, A.The minima of indefinite quaternary quadratic forms. Ann. Math. 32 (1931), 271–298.CrossRefGoogle Scholar
(15)Oppenheim, A.Value of quadratic forms III. Monats. Math. 57 (1953), 97–101.CrossRefGoogle Scholar
(16)Oppenheim, A.Value of quadratic forms I. Quart. J. Math. Oxford (2) 4 (1953), 54–59.CrossRefGoogle Scholar
(17)Watson, G. L.Indefinite quadratic polynomials. Mathematika 7 (1960), 141–144.CrossRefGoogle Scholar
(18)Watson, G. L.Indefinite quadratic forms in many variables: The inhomogeneous minimum and a generalization. Proc. Lond. Math. Soc. (3) 12 (1962), 564–576.CrossRefGoogle Scholar
(19)Watson, G. L.Asymmetric inequalities for indefinite quadratic forms. Proc. Lond. Math. Soc. 18 (1968), 95–113.CrossRefGoogle Scholar