On a singular eigenvalue problem
Published online by Cambridge University Press: 24 October 2008
Extract
Sears and Titchmarsh (1) have formulated an expansion in eigenfunctions which requires a knowledge of the s-zeros of the equation
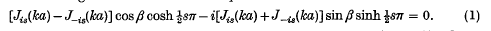
Here ka > 0 is supposed given and β is a real constant such that 0 ≤ β < π. The above equation is encountered when one seeks the eigenfunctions of the differential equation
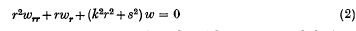
on the interval 0 < α ≤ r < ∞ subject to the condition of vanishing at r = α. Solutions of (2) are the Bessel functions J±is(kr) and every solution w of (2) is such that r−½w(r) belongs to L2 (α, ∞). Since the problem is of the limit circle type at infinity it is necessary to prescribe a suitable asymptotic condition there to make the eigenfunctions determinate. In the present instance this condition is
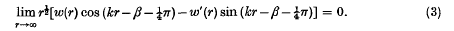
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 2 , April 1968 , pp. 439 - 446
- Copyright
- Copyright © Cambridge Philosophical Society 1968
References
REFERENCES
- 1
- Cited by

