Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-24T05:59:35.800Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Sturm-Liouville expansion in series of Bessel functions

Published online by Cambridge University Press:  24 October 2008

D. Naylor
D. Naylor
Affiliation:
Department of Mathematics, University of Western Ontario
Get access Rights & Permissions [Opens in a new window]

Extract

1. The determination of potentials and wave functions defined in regions bounded by the natural coordinate surfaces of a cylindrical polar coordinate system leads to eigenvalue problems connected with Bessel's differential equation

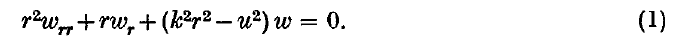
We shall consider the annulus 0 < a ≤ r ≤ b and take first the boundary condition to be that of vanishing on both surfaces. It is then convenient to introduce the function

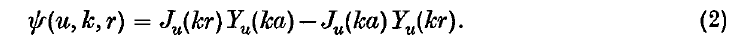
This function will automatically satisfy the condition of vanishing for r = a. It will also vanish on r = b if u and k are related by the condition that ψ(u, k, b) = 0. If we regard u as being fixed and real then there will be an infinite number of zeros kn(u)(n = 1,2,…).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 1 , January 1966 , pp. 61 - 72
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bridge, J. F. and Angrist, S. W. An extended table of roots of Math. Comp. 16 (1962), 198–204.Google Scholar
(2)British Association for the Advancement of Science. Bessel functions, Part I (Functions of order zero and unity). Mathematical tables, vol. vi (Cambridge, 1950).Google Scholar
(3)Chandrasekhar, S. and Elbert, D.Roots of Yn(λη) Jn(λ)−Jn(λη) Yn(λ) = 0. Proc. Cambridge Philos. Soc. 50 (1954), 266–268.CrossRefGoogle Scholar
(4)Dwight, H. B.Tables of roots for natural frequencies in coaxial type cavities. J. Math. and Phys. 27 (1948), 84–89.CrossRefGoogle Scholar
(5)Fletcher, A., Mules, J. C. P., Rosenhead, L. and Comrie, L. J.An index of mathematical tables, 2nd ed. (Adison Wesley, 1962).Google Scholar
(6)Gray, A. and Mathews, G. B.A treatise on Bessel functions, 2nd ed. (Macmillan, 1922).Google Scholar
(7)McMahon, J.On the roots of Bessel and certain related functions. Ann. of Math. (1), 9 (1895), 23–30.CrossRefGoogle Scholar
(8)National Bureau of Standards. Handbook of mathematical functions (Washington, 1964).Google Scholar
(9)Naylor, D.An eigenvalue problem in cylindrical harmonics. J. Math. and Phys. 44 (1965). To appear.CrossRefGoogle Scholar
(10)Titchmarsh, E. C.A class of expansions in series of Bessel functions. Proc. London Math, Soc. 22 (1922), xiii–xvi.Google Scholar
(11)Truell, R.Concerning the roots of J′n(x) N′n(kx)−J′n(kx) N′n(x) = 0. J. Appl. Phys. 14 (1943), 350–352.CrossRefGoogle Scholar
(12)Watson, G. N.A treatise on the theory of Bessel functions, 2nd ed. (Cambridge, 1944), pp. 507–510.Google Scholar
(13)Willis, D. M.A property of the zeros of a cross product of Bessel functions. Proc. Camb. Phil. Soc. 61 (1965), 425–428.CrossRefGoogle Scholar
(14)Cochran, J. A.Remarks on zeros of cross product Bessel functions. J. Soc. Ind. Appl. Math. 12 (1964), 580–587.CrossRefGoogle Scholar