No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
1. It has been observed that certain problems in quantum mechanics have their exact solutions which can be expressed in terms of Appell's function F2 as defined by (e.g. (7), p. 211)
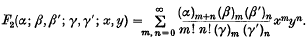
Having regard to this fact, Srivastava (5) proved a summation formula
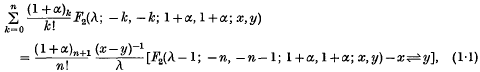
where R(λ) > 1, R(α) > − 1 and x⇌y indicates the presence on the right of a second term that originates from the first by interchanging x and y.