Published online by Cambridge University Press: 10 July 2018
Let K be a field of characteristic zero and let R = K[X1, . . .,Xn], with standard grading. Let 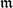 ${\mathfrak m}$ = (X1, . . ., Xn) and let E be the *injective hull of R/
${\mathfrak m}$ = (X1, . . ., Xn) and let E be the *injective hull of R/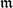 ${\mathfrak m}$. Let An(K) be the nth Weyl algebra over K. Let I, J be homogeneous ideals in R. Fix i, j ≥ 0 and set M = HiI(R) and N = HjJ(R) considered as left An(K)-modules. We show the following two results for which no analogous result is known in charactersitc p > 0.
${\mathfrak m}$. Let An(K) be the nth Weyl algebra over K. Let I, J be homogeneous ideals in R. Fix i, j ≥ 0 and set M = HiI(R) and N = HjJ(R) considered as left An(K)-modules. We show the following two results for which no analogous result is known in charactersitc p > 0.
(i) 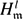 $H^l_{\mathfrak m}$(TorRν(M, N)) ≅ E(n)al,ν for some al,ν ≥ 0.
$H^l_{\mathfrak m}$(TorRν(M, N)) ≅ E(n)al,ν for some al,ν ≥ 0.
(ii) For all ν ≥ 0; the finite dimensional vector space TorAn(K)ν(M♯, N) is concentrated in degree -n (here M♯ is the standard right An(K)-module associated to M).