Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kamiya, Shigeyasu
2000.
Proceedings of the Second ISAAC Congress.
Vol. 8,
Issue. ,
p.
1149.

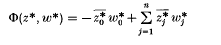
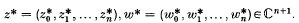 . We can regard an element of
. We can regard an element of 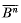 , where
, where