Published online by Cambridge University Press: 24 October 2008
Let
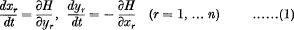
be a system of differential equations of Hamiltonian form, the characteristic function H being independent of t and expansible in a convergent series of powers of x1, … xn, y1, … yn in which the terms of lowest degree are
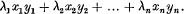
* The coefficients in this transformation are not necessarily real.
† If the origin had been an ordinary point of the equations there would have been 2n − 1 integrals developable about it. See p. 273, above, “Integrals of Systems of Ordinary Differential Equations.”
* ”On the Adelphic Integral of the Differential Equations of Dynamics” (Proc. Roy. Soc. Edin., November, 1916).Google Scholar
* Whittaker, , Analytical Dynamics (2nd ed.), § 146.Google Scholar
* Here, and in (c) below, we consider only the general case; this is sufficient for illustrative purposes, since we are only verifying a result which we know from § 3, that the coefficients of all critical terms vanish.
† It is supposed that the terms ø1, ø2, ø3, ø4 are all different and that none of D 1, D 2, D 12, D 13, … vanishes.
* This determinant has the value ![]() and is non-zero because
and is non-zero because ![]() and, from (59),
and, from (59), ![]()
† Whittaker, , Analytical Dynamics (2nd ed.), § 130.Google Scholar
* If n = 2 and the ratio λ1: λ2 is not real the modulus of the expression (63) has a definite non-zero lower bound for all possible integral choices of A 1, A 2 except A 1 = A 2=0; if n=2 and λ1: λ2 is real, or if n > 2, the lower bound is zero and the statement in the text is valid.
* I.e. products of powers of x 1y 1, x 2y 2, … x ny n.
† Thus
but though the two sserie on the right are divergent for ![]() we cannot conclude the same range of divergence for the series on the left, which is in fact convergent for | x | <1.
we cannot conclude the same range of divergence for the series on the left, which is in fact convergent for | x | <1.
* Arising in the problem of the motion of a rigid body about a fixed point under no forces; q is the constant in an angular momentum integral by means of which the number of degrees of freedom has been reduced from 3 to 2.
† Since H enters the equations only through its derivatives, the presence of the constant term q 2/2A is immaterial.