No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let Γ be a discrete subgroup of G = PSL(2,ℝ) and p be the canonical map from the universal covering group 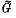 on to PSL(2,ℝ). By a continuity argument on a fundamental polygon for Γ acting on the hyperbolic plane
on to PSL(2,ℝ). By a continuity argument on a fundamental polygon for Γ acting on the hyperbolic plane 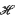 2, Milnor (4) obtained a presentation for p−1(Γ) whenever
2, Milnor (4) obtained a presentation for p−1(Γ) whenever 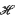 2/Γ is compact and of genus zero. Using Teichmüller theory and a double Reidemeister-Schreier process, Macbeath(2) showed that the general compact case can be deduced from Milnor's result. We give here a method of obtaining a presentation which uses only the geometry of a Dirichlet region and which applies equally to the non-compact case.
2/Γ is compact and of genus zero. Using Teichmüller theory and a double Reidemeister-Schreier process, Macbeath(2) showed that the general compact case can be deduced from Milnor's result. We give here a method of obtaining a presentation which uses only the geometry of a Dirichlet region and which applies equally to the non-compact case.