Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
GRUBER, Peter M.
1993.
Handbook of Convex Geometry.
p.
319.
LINDENSTRAUSS, J.
and
MILMAN, V.D.
1993.
Handbook of Convex Geometry.
p.
1149.
FLORIAN, A.
1993.
Handbook of Convex Geometry.
p.
177.
Gruber, P. M.
1994.
Polytopes: Abstract, Convex and Computational.
p.
173.
Ambrosio, Luigi
and
Kirchheim, Bernd
2000.
Currents in metric spaces.
Acta Mathematica,
Vol. 185,
Issue. 1,
p.
1.
Preiss, David
2003.
Vol. 2,
Issue. ,
p.
1519.
Düvelmeyer, Nico
2005.
Angle Measures and Bisectors in Minkowski Planes.
Canadian Mathematical Bulletin,
Vol. 48,
Issue. 4,
p.
523.
Bronstein, E. M.
2008.
Approximation of convex sets by polytopes.
Journal of Mathematical Sciences,
Vol. 153,
Issue. 6,
p.
727.
Ostrovskii, M.I.
2008.
Sufficient enlargements of minimal volume for finite-dimensional normed linear spaces.
Journal of Functional Analysis,
Vol. 255,
Issue. 3,
p.
589.
Henk, Martin
Linke, Eva
and
Wills, Jörg M.
2010.
Minimal zonotopes containing the crosspolytope.
Linear Algebra and its Applications,
Vol. 432,
Issue. 11,
p.
2942.
Ostrovskii, M. I.
2011.
Auerbach Bases and Minimal Volume Sufficient Enlargements.
Canadian Mathematical Bulletin,
Vol. 54,
Issue. 4,
p.
726.
Martini, Horst
and
Wu, Senlin
2014.
Classical curve theory in normed planes.
Computer Aided Geometric Design,
Vol. 31,
Issue. 7-8,
p.
373.
Brazitikos, Silouanos
2017.
BRASCAMP–LIEB INEQUALITY AND QUANTITATIVE VERSIONS OF HELLY'S THEOREM.
Mathematika,
Vol. 63,
Issue. 1,
p.
272.
Babenko, Ivan
and
Massart, Daniel
2017.
On systolic zeta functions.
European Journal of Mathematics,
Vol. 3,
Issue. 4,
p.
899.
Galicer, Daniel
Merzbacher, Mariano
and
Pinasco, Damián
2019.
The Minimal Volume of Simplices Containing a Convex Body.
The Journal of Geometric Analysis,
Vol. 29,
Issue. 1,
p.
717.
Fodor, Ferenc
Naszódi, Márton
and
Zarnócz, Tamás
2019.
On the volume bound in the Dvoretzky–Rogers
lemma.
Pacific Journal of Mathematics,
Vol. 301,
Issue. 1,
p.
89.
Bezdek, Károly
and
Lángi, Zsolt
2019.
Minimizing the mean projections of finite
$$\rho $$
ρ
-separable packings.
Monatshefte für Mathematik,
Vol. 188,
Issue. 4,
p.
611.
Merino, Bernardo González
and
Schymura, Matthias
2020.
On the reverse isodiametric problem and Dvoretzky–Rogers-type volume bounds.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 3,
Khrabrov, A.
and
S. V. Kislyakov
2021.
Volume ratios for Cartesian products of convex bodies.
St. Petersburg Mathematical Journal,
Vol. 32,
Issue. 5,
p.
905.
Hong, David E.
Ismailescu, Dan
Kwak, Alex
and
Park, Grace Y.
2023.
On the smallest area $$(n-1)$$-gon containing a convex n-gon.
Periodica Mathematica Hungarica,
Vol. 87,
Issue. 2,
p.
394.
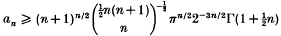
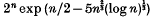
 . We show that
. We show that 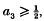 , and that a local minimum of the function C→a(C) for C ⊂ ℝn is attained only at an equiframed convex body (that is, a body such that every point of its boundary belongs to a parallelepiped of minimal volume containing the body).
, and that a local minimum of the function C→a(C) for C ⊂ ℝn is attained only at an equiframed convex body (that is, a body such that every point of its boundary belongs to a parallelepiped of minimal volume containing the body).

