On polycyclic groups with isomorphic finite quotients
Published online by Cambridge University Press: 24 October 2008
Extract
Following P. F. Pickel (5) we write 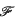 (G) for the set of isomorphism classes of finite quotients of a group G. One of the outstanding problems in the theory of polycyclic groups is to determine whether there can be infinitely many non-isomorphic polycyclic groups G with a given
(G) for the set of isomorphism classes of finite quotients of a group G. One of the outstanding problems in the theory of polycyclic groups is to determine whether there can be infinitely many non-isomorphic polycyclic groups G with a given 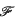 (G). We solve a special case of this problem with our first main result:
(G). We solve a special case of this problem with our first main result:
Theorem 1. Let G be an abelian-by-cyclic polycyclic group. Then the polycyclic-by-finite groups H with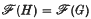 lie in only finitely many isomorphism classes.
lie in only finitely many isomorphism classes.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 84 , Issue 2 , September 1978 , pp. 235 - 246
- Copyright
- Copyright © Cambridge Philosophical Society 1978
References
REFERENCES
- 3
- Cited by


