Published online by Cambridge University Press: 24 October 2008
Let σs(n) denote the sum of the sth powers of the divisors of n,

and let 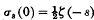 , where ζ(s) is the Riemann ζfunction. Ramanujan, in his paper “On certain arithmetical functions*”, proves that, if
, where ζ(s) is the Riemann ζfunction. Ramanujan, in his paper “On certain arithmetical functions*”, proves that, if
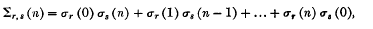
and

then 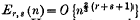 , whenever r and s are odd positive integers. He conjectures that the error term on the right of (1·1) is of the form
, whenever r and s are odd positive integers. He conjectures that the error term on the right of (1·1) is of the form

for every ε > 0, and that it is not of the form 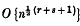 . He further conjectures that
. He further conjectures that

for all positive values of r and s; and this conjecture has recently been proved to be correct.
* Trans. Camb. Phil. Soc. 22 (1916), 159–184;Google ScholarCollected Papers, No. 18. It is to be observed, in (1·1), that ζ(1-r)=0 if r≠=1, ζ(0)=−½.
† Ingham, A. E., Journal London Math. Soc. 2 (1927), 202–208.CrossRefGoogle Scholar
‡ Ramanujan, , loc. cit.Google Scholar; Hardy, Q. H., Proc. Camb. Phil. Soc. 23 (1927), 675–680.CrossRefGoogle Scholar
* The error term is then actually zero—as also when r + s is equal to 4, 6, 8 or 12.
† Wigert, S., Acta Math. 37, (1914), p. 113–140.CrossRefGoogle Scholar
‡ Compare Hardy, and Ramanujan, , “Asymptotic formulae in combinatory analysis”, Proc. London Math. Soc. (2) 17 (1918), 75–115, Lemma 4·31;CrossRefGoogle Scholar Ramanujan's Collected Papers, No. 36.
* In particular (0, q) = q.Google Scholar
† Vorlesungen über Zahlentheorie (1927), 1, 217–218.Google Scholar
* It is a corollary from (2·32) and the transformation equation of the modular function
that Ramanujan's function τ (n) is O(n 6).—Hardy, loc. cit.
* For the proof of (2·51) see, for example, Landau, loc. cit. 1, 188. The inner sum is to be taken over the common divisors d of q and n.Google Scholar
* The case k = 1 leads merely to an identity.Google Scholar
* When h = k, the term v = k; is merely a repetition of that for which v = k − 1.Google Scholar
† It is not, in general, true (as it is when k = 2) that Q 1(x) disappears from this polynomial.Google Scholar
‡ Hardy, , loc. cit.Google Scholar
* It is true when k = 2, as Ramanujan shows.Google Scholar
† I require one additional entry in the case of Σ1117(n).Google Scholar
‡ T(n)= Er, s(n)/Er, s(1) if r + s = 14.—Ramanujan, loc. cit., equation (95).
* For a remarkable deduction from, this congruence—a deduction stated and partly proved by Ramanujan—see Miss Stanley, G. K., “Two assertions made by Ramanujan”, Journal London Math. Soc. 3 (1928), 232–237, where, on p. 235, 1. 8 from the end, “number of” should read “sum of the”.CrossRefGoogle Scholar
† This relation follows immediately from equation (1·63) of Ramanujan's posthumous paper, “Congruence properties of partitions”, Math. Zeitschrift, 9 (1921), 147–153 (Collected Papers, No. 30), but Ramanujan does not seem to have noticed the fact. The same formula (1·63) occurs as line 6 of Table I of the paper “On certain arithmetical functions”, No. 18.CrossRefGoogle Scholar
‡ This relation was conjectured by Ramanujan and was subsequently proved by Mordell, , Proc. Camb. Phil. Soc. 19 (1919), 117–124.Google Scholar
§ Mordell, , loc. cit. 119, equation (4), in which κ = 16, ξ = 1.Google Scholar