No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
For cardinal numbers λ, K, ∑ a (λ, K)-family is a family of sets  such that |
such that | | =
| =  and |A| = K for every A ε
and |A| = K for every A ε  , and a (λ, K, ∑)-family is a (λ,K)-family
, and a (λ, K, ∑)-family is a (λ,K)-family  such that |∪
such that |∪ | = ∑. Two sets A, B are said to be almost disjoint if
| = ∑. Two sets A, B are said to be almost disjoint if
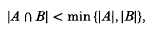
and an almost disjoint family of sets is a family whose members are pairwise almost disjoint. A representing set of a family  is a set X ⊆ ∪
is a set X ⊆ ∪  such that X ∩ A = ⊘ for each A ε
such that X ∩ A = ⊘ for each A ε  . If
. If  is a family of sets and |∪
is a family of sets and |∪ | = ∑, then we write
| = ∑, then we write 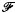 εADR(
εADR( ) to signify that
) to signify that 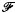 is an almost disjoint family of ∑-sized representing sets of
is an almost disjoint family of ∑-sized representing sets of  . Also, we define a cardinal number
. Also, we define a cardinal number