No CrossRef data available.
On Self-reciprocal functions for Fourier-Bessel integral transforms
Published online by Cambridge University Press: 24 October 2008
Extract
Following Hardy and Titchmarsh(1) a function f(x) is said to be self-reciprocal if it satisfies the Fourier-Bessel integral transform
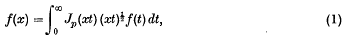
where Jp(x) is a Bessel function of order P ≥ –½. This integral is denoted by Rp. The special cases P ½ and P ½, we denote by Rs and Rc, respectively.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 4 , October 1961 , pp. 778 - 781
- Copyright
- Copyright © Cambridge Philosophical Society 1961
References
REFERENCES
(1)Hardy, G. H. and Titchmarsh, E. C., Self reciprocal functions. Quart. J. Math. (2), 1 (1930), 196–231.Google Scholar
(2)Lakshmikanth, V. On the relation between the self-reciprocal functions and kernels (submitted for publication).Google Scholar
(3)Lakshmikanth, V., Some self-reciprocal functions. Proc. Nat. Acad. Sci. (India), Part A, 28 (1959), 246–8.Google Scholar
(4)Lakshmikanth, V., Some self-reciprocal functions and kernels. Proc. Camb. Phil. Soc. 57 (1961), 690–2.Google Scholar
(5)Wills, H. F., A formula for expanding an integral as series. Phil. Mag. (7), 39 (1948), 455–9.Google Scholar


