Published online by Cambridge University Press: 24 October 2008
Solutions of the partial differential equation ψzzzz + ψx + 0 of the type ψ = x¼nw(y), where y = zx−¼ and n is an integer, are investigated. The equation occurs as a boundary-layer approximation in certain rotating and stratified fluid flows in which the production of vorticity (due, for example, to changes in the Coriolis parameter with latitude in two-dimensional flows on a beta plane, or by the buoyant generation of vorticity in a Boussinesq fluid) is opposed by a diffusive process. The similarity functions w(y) satisfy the fourth order differential equation
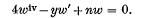 .
.
These functions have many properties analogous to those of error functions and parabolic cylinder functions. When n is a non-negative integer, there exist polynomial solutions of the latter equation. These have analogies with Hermite polynomials, although they do not form an orthogonal set in any useful sense. The main properties of the similarity functions are listed, including their series expansions, integral representations, asymptotic expansions and recurrence relations. In particular, a pair of independent solutions, Jon(y) and Kon(y), are denned such that Jon(y) and Kon(y) are real for real y and vanish at an exponential rate as y → + ∞. The function Jon(y) also decays exponentially as y → − ∞ if n is negative, and grows algebraically as y → − ∞ if n is positive. Curves of the functions Jon(y) and Kon(y) are given for |n| ≤ 3 and 0 < y < 6, and their more useful properties are listed.