Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T14:19:23.100Z Has data issue: false hasContentIssue false
  • English
  • Français

On the bivariate Erdős–Kac theorem and correlations of the Möbius function

Part of: Multiplicative number theory

Published online by Cambridge University Press:  14 August 2019

ALEXANDER P. MANGEREL
ALEXANDER P. MANGEREL*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, Canada. e-mail: smangerel@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a positive integer n let ω (n) denote the number of distinct prime factors of n, and let a be fixed positive integer. Extending work of Kubilius, we develop a bivariate probabilistic model to study the joint distribution of the deterministic vectors (ω(n), ω(n + a)), with n ≤ x as x → ∞, where n and n + a belong to a subset of ℕ with suitable properties. We thus establish a quantitative version of a bivariate analogue of the Erdős–Kac theorem on proper subsets of ℕ.

We give three applications of this result. First, if y = x0(1) is not too small then we prove (in a quantitative way) that the y-truncated Möbius function μy has small binary autocorrelations. This gives a new proof of a result due to Daboussi and Sarkőzy. Second, if μ(n; u) :=e(uω(n)), where u ∈ ℝ then we show that μ(.; u) also has small binary autocorrelations whenever u = o(1) and 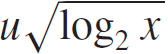$u\sqrt {\mathop {\log }\nolimits_2 x} \to \infty$, as x → ∞. These can be viewed as partial results in the direction of a conjecture of Chowla on binary correlations of the Möbius function.

Our final application is related to a problem of Erdős and Mirsky on the number of consecutive integers less than x with the same number of divisors. If 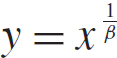$y = x^{{1 \over \beta }}$, where β = β(x) satisfies certain mild growth conditions, we prove a lower bound for the number of consecutive integers n ≤ x that have the same number of y-smooth divisors. Our bound matches the order of magnitude of the one conjectured for the original Erdős-Mirsky problem.

MSC classification

Primary: 11N36: Applications of sieve methods 11N60: Distribution functions associated with additive and positive multiplicative functions
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 3 , November 2020 , pp. 547 - 605
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cassaigne, J., Ferenczi, S., Mauduit, C., Rivat, J. and Sarkőzy, A.. On finite pseudorandom binary sequences. III. The Liouville function. I. Acta Arithmetica 87(4) (1999), 367–390.Google Scholar
Chowla, S.. The Riemann Hypothesis and Hilbert’s Tenth Problem (Gordon and Breach Science Publishers, New York-London-Paris, 1965).Google Scholar
Daboussi, H. and Sarkőzy, A.. On the correlation of the truncated Liouville function. Acta Arith. 108 (2003), 61–76.Google Scholar
Tenenbaum, G. and Fouvry, É.. Répartition statistiques des entiers sans grand facteur premier dans les progressions arithmétiques. Proc. London Math. Soc. 72(3) (1996), 481–514.Google Scholar
Elliott, P.D.T.A.. Probabilistic Number Theory I (Springer-Verlag, New York, U.S.A, 1979).CrossRefGoogle Scholar
Erdős, P.. On the integers having exactly k prime factors. Ann. Math. 49 (1948), 53–66.CrossRefGoogle Scholar
Erdős, P. and Mirsky, L.. The distribution of values of the divisor function d(n). Proc. London Math. Soc. 3 (1952), 257–271.Google Scholar
Erdős, P., Pomerance, C. and Sarkőzy, A.. On locally repeated values of certain arithmetic functions III. Proc. Amer. Math. Soc. 101 (1987), 1–7.Google Scholar
Esséen, C.–G.. On the Lyapunov limit of error in the theory of probability. Arkiv för matematik, Astronomi och Fysik A28 (1942), 1–19.Google Scholar
Feller, W.. An Introduction to Probability Theory and its Applications Vol. 2 (Wiley Publishing, New York, NY, 1957).Google Scholar
Friedlander, J. and Iwaniec, H.. Opera de Cribro (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Ganguli, H.. On the correlation of completely multiplicative functions. PhD. thesis. Simon Fraser University, Vancouver, Canada (2013).Google Scholar
Granville, A. and Soundararajan, K.. Sieving and the Erdős–Kac theorem, pages 15–27 (Springer Netherlands, Dordrecht, 2007).Google Scholar
Halász, G.. On the distribution of additive arithmetic functions. Acta Arith. 27 (1975), 143–152.CrossRefGoogle Scholar
Heath–brown, D.R.. The divisor function at consecutive integers. Mathematika 31(1) (1984), 141–149.CrossRefGoogle Scholar
Heath–brown, D.R.. The square sieve and consecutive square-free numbers. Math. Ann. 266 (1984), 251–260.Google Scholar
Hildebrand, A.. The divisor function at consecutive integers. Pachi J. Math. 129 (1987), 307–319.CrossRefGoogle Scholar
Kubilius, J.. Probabilistic methods in the theory of numbers. AMS, Translations of Mathematical Monographs (Providence, RI, 1964).Google Scholar
Leveque, W.. On the size of certain number-theroetic functions. Trans. Amer. Math. Soc. 65 (1949), 440–463.CrossRefGoogle Scholar
Matomäki, K. and Radziwiłł, M.. Multiplicative functions in short intervals. Ann. of Math 183 (2016), 1015–1056.CrossRefGoogle Scholar
Matomäki, K., Radziwill, M. and Tao, T.. An averaged form of Chowla’s conjecture. Algebra and Number Theory 9 (2015), 2167–2196.CrossRefGoogle Scholar
Rényi, A. and Turán, P.. On a theorem of Erdos–Kac. Acta Arith. 4 (1958), 71–84.CrossRefGoogle Scholar
Roos, B.. Metric multivariate Poisson approximation of the generalised multinomial distribution. Teor. Veroyatnost. i Primenen 43 (1998), 404–413.CrossRefGoogle Scholar
Sadikova, S.M.. On two-dimensional analogs of an inequality of k.g. esseen and their application to the central limit theorem. Theory Probab. Appl. 11(3) (1966), 369–380.CrossRefGoogle Scholar
Tao, T.. The logarithmically averaged Chowla and Elliott conjectures for two-point correlations. Forum Math. Pi 4 (2016), 36pp.CrossRefGoogle Scholar
Tenenbaum, G.. Introduction to Analytic and Probabilistic Number Theory (Cambridge University Press, Cambridge, UK, 1994).Google Scholar