Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mourougane, Christophe
and
Russo, Francesco
1997.
Some remarks on nef and good divisors on an algebraic variety.
Comptes Rendus de l'Académie des Sciences - Series I - Mathematics,
Vol. 325,
Issue. 5,
p.
499.


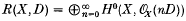 . As is known, for a semi-ample divisor
. As is known, for a semi-ample divisor 