On the convex kernel of a compact set
Published online by Cambridge University Press: 24 October 2008
Extract
Suppose that E is a compact subset of a topological linear space ℒ. Then the convex kernel K, of E, is such that a point k belongs to K if every point of E can be seen, via E, from k. Valentine (l) has asked for conditions on E which ensure that the convex kernel K, of E, consists of exactly one point, and in this note we give such a condition. If A, B, C are three subsets of E, we use (A, B, C) to denote the set of those points of E, which can be seen, via E, from a triad of points a, b, c, with a ∈ A, b ∈ B, c ∈ C. We shall say that E has the property 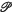 if, whenever A is a line segment and B, C are points of E which are not collinear with any point of A, the set (A, B, C) has linear dimension of at most one, and degenerates to a single point whenever A is a point.
if, whenever A is a line segment and B, C are points of E which are not collinear with any point of A, the set (A, B, C) has linear dimension of at most one, and degenerates to a single point whenever A is a point.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 2 , April 1967 , pp. 311 - 313
- Copyright
- Copyright © Cambridge Philosophical Society 1967
References
REFERENCE
- 2
- Cited by


