Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T04:55:59.701Z Has data issue: false hasContentIssue false
  • English
  • Français

On the generalizations of the theorems of Parseval and Riesz-Fischer

Published online by Cambridge University Press:  24 October 2008

S. Pollard
S. Pollard
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

Any two real numbers p and q will be called conjugate if

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 8 , October 1927 , pp. 865 - 870
Copyright
Copyright © Cambridge Philosophical Society 1927

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

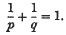
* Hobson, E. W., Theory of Functions of a Real Variable, 2 (1926), 599–606.Google Scholar

* By (4·1) is to be understood that f(x) = g(x) throughout −π ≤ x ≤ π except possibly at the points of a set of measure zero.

* Banach, S., Proc. London Math. Soc. (2) 21 (1923), 95–97. Banach assumes that f(x) is positive and so absolutely integrable. It is interesting to verify that his construction can be extended to the case of conditionally integrable functions.CrossRefGoogle Scholar