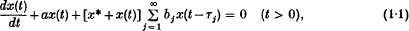Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gopalsamy, K.
1987.
A simple stability criterion for a linear system of neutral integro-differential equations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 102,
Issue. 01,
p.
149.
Gopalsamy, K
and
Zhang, B. G.
1988.
On a neutral delay logistic equation.
Dynamics and Stability of Systems,
Vol. 2,
Issue. 3-4,
p.
183.
Krisztin, Tibor
1990.
Stability for functional-differential equations and some variational problems.
Tohoku Mathematical Journal,
Vol. 42,
Issue. 3,
1993.
Delay Differential Equations - With Applications in Population Dynamics.
Vol. 191,
Issue. ,
p.
353.
Kowalczyk, R.
and
Foryś, U.
2002.
Qualitative analysis on the initial value problem to the logistic equation with delay.
Mathematical and Computer Modelling,
Vol. 35,
Issue. 1-2,
p.
1.
Muroya, Yoshiaki
2007.
A global stability criterion in nonautonomous delay differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 1,
p.
209.
Muroya, Yoshiaki
2007.
Global stability for separable nonlinear delay differential systems.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 1,
p.
372.
Bozkurt, F.
2013.
Hopf Bifurcation and Stability Analysis for A Delayed Logistic Equation.
International Journal of Modeling and Optimization,
p.
288.
Agarwal, Ravi P.
O’Regan, Donal
and
Saker, Samir H.
2014.
Oscillation and Stability of Delay Models in Biology.
p.
293.