Article contents
On the intersection of free subgroups in free products of groups
Published online by Cambridge University Press: 01 May 2008
Abstract
Let (Gi | i ∈ I) be a family of groups, let F be a free group, and let  the free product of F and all the Gi.
the free product of F and all the Gi.
Let 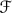 denote the set of all finitely generated subgroups H of G which have the property that, for each g ∈ G and each i ∈ I,
denote the set of all finitely generated subgroups H of G which have the property that, for each g ∈ G and each i ∈ I, 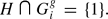 By the Kurosh Subgroup Theorem, every element of
By the Kurosh Subgroup Theorem, every element of 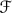 is a free group. For each free group H, the reduced rank of H, denoted r(H), is defined as
is a free group. For each free group H, the reduced rank of H, denoted r(H), is defined as 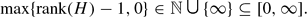 To avoid the vacuous case, we make the additional assumption that
To avoid the vacuous case, we make the additional assumption that 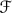 contains a non-cyclic group, and we define
contains a non-cyclic group, and we define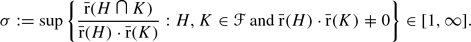 We are interested in precise bounds for
We are interested in precise bounds for 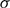 . In the special case where I is empty, Hanna Neumann proved that
. In the special case where I is empty, Hanna Neumann proved that 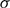 ∈ [1,2], and conjectured that
∈ [1,2], and conjectured that 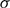 = 1; fifty years later, this interval has not been reduced.
= 1; fifty years later, this interval has not been reduced.
With the understanding that ∞/(∞ − 2) is 1, we define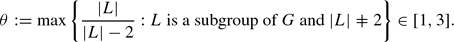
Generalizing Hanna Neumann's theorem we prove that 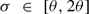 , and, moreover,
, and, moreover, 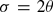 whenever G has 2-torsion. Since
whenever G has 2-torsion. Since 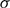 is finite,
is finite, 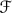 is closed under finite intersections. Generalizing Hanna Neumann's conjecture, we conjecture that
is closed under finite intersections. Generalizing Hanna Neumann's conjecture, we conjecture that 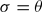 whenever G does not have 2-torsion.
whenever G does not have 2-torsion.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 3 , May 2008 , pp. 511 - 534
- Copyright
- Copyright © Cambridge Philosophical Society 2008
References
REFERENCES
- 13
- Cited by


