Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yang, Hsun‐Tiao
and
Lees, Lester
1956.
Rayleigh's Problem at Low Mach Number According to the Kinetic Theory of Gases.
Journal of Mathematics and Physics,
Vol. 35,
Issue. 1-4,
p.
195.
Yasuhara, Michiru
1957.
On the Hypersonic Viscous Flow past a Flat Plate with Suction or Injection.
Journal of the Physical Society of Japan,
Vol. 12,
Issue. 2,
p.
177.
Cox, R. N.
1959.
General Characteristics of Hypersonic Flow Fields.
The Journal of the Royal Aeronautical Society,
Vol. 63,
Issue. 585,
p.
503.
1959.
Hypersonic Flow Theory.
Vol. 5,
Issue. ,
p.
417.
Hromas, Leslie
and
Degroff, Harold
1959.
Experimental search for the effect of compressibility in unsteady Couette flow.
Journal of Fluid Mechanics,
Vol. 5,
Issue. 01,
p.
140.
Stewartson, K.
1960.
Advances in Applied Mechanics Volume 6.
Vol. 6,
Issue. ,
p.
1.
Harlow, Francis H.
and
Meixner, Billy D.
1961.
Motion of a Viscous Compressible Gas Adjacent to a Sliding Plate.
The Physics of Fluids,
Vol. 4,
Issue. 10,
p.
1202.
Traugott, S. C.
1962.
Impulsive motion of an infinite plate in a compressible fluid with non-uniform external flow.
Journal of Fluid Mechanics,
Vol. 13,
Issue. 3,
p.
400.
Sone, Yoshio
1964.
Kinetic Theory Analysis of Linearized Rayleigh Problem.
Journal of the Physical Society of Japan,
Vol. 19,
Issue. 8,
p.
1463.
DEWEY, JR., C.
1965.
Bluntness and viscous-interaction effects on slender bodies at hypersonic speeds.
Wuest, W.
1967.
Boundary layers in rarefied gas flow.
Progress in Aerospace Sciences,
Vol. 8,
Issue. ,
p.
295.
Solan, Alexander
and
Cohen, Ira M.
1967.
Rayleigh Problem in a Radiating Compressible Gas I. Plate Mach Number Finite.
The Physics of Fluids,
Vol. 10,
Issue. 1,
p.
108.
Solan, Alexander
and
Cohen, Ira M.
1967.
Rayleigh Problem in a Radiating Compressible Gas. II. Plate Mach Number Large.
The Physics of Fluids,
Vol. 10,
Issue. 2,
p.
257.
Davies, W. R.
and
Bernstein, L.
1969.
Heat transfer and transition to turbulence in the shock-induced boundary layer on a semi-infinite flat plate.
Journal of Fluid Mechanics,
Vol. 36,
Issue. 1,
p.
87.
Chang, T S
and
Chang, C M
1971.
Rayleigh's problem in collisionless plasmas.
Plasma Physics,
Vol. 13,
Issue. 9,
p.
695.
Petrova, L. I.
and
Ryzhov, O. S.
1972.
Hypersonic viscous gas flow past half-bodies.
Fluid Dynamics,
Vol. 4,
Issue. 1,
p.
43.
Thompson, B. W.
1975.
Proceedings of the Fourth International Conference on Numerical Methods in Fluid Dynamics.
Vol. 35,
Issue. ,
p.
397.
1984.
Shocks generated in a confined gas due to rapid heat addition at the boundary. II. Strong shock waves.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 393,
Issue. 1805,
p.
331.
Min Hyun, Jae
and
Sang Park, Jun
1989.
Some Aspects of Compressible Rayleigh's Problem in a Rotating Cylinder.
Journal of the Physical Society of Japan,
Vol. 58,
Issue. 1,
p.
159.
Min Hyun, Jae
and
Sang Park, Jun
1990.
Early-Time Behavior of the Ekman Layers in Spin-Up of a Rapidly-Rotating Gas.
Journal of the Physical Society of Japan,
Vol. 59,
Issue. 10,
p.
3584.
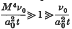 log M, where ν0 is the coefficient of kinematic viscosity of the undisturbed air. An approximate method is also given to enable the solution to be joined up to Van Dyke's (10) which is valid when
log M, where ν0 is the coefficient of kinematic viscosity of the undisturbed air. An approximate method is also given to enable the solution to be joined up to Van Dyke's (10) which is valid when 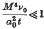 .
.