On the solution of certain integral equations by generalized functions
Published online by Cambridge University Press: 24 October 2008
Extract
This note is concerned with a method by which generalized solutions can be shown to exist for certain types of integral equations
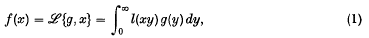
where f(x) ∈ L2(0, ∞). The method is briefly this. An extended meaning is given to such equations by using generalized functions of a particular type. Then, if (1) denotes a transformation which has no everywhere-defined inverse in the usual sense, it may be possible to define in the extended sense an inverse transformation
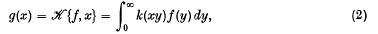
so that if f is given, a generalized function g = 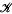 can be determined as a solution of (1).
can be determined as a solution of (1).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 4 , October 1961 , pp. 767 - 777
- Copyright
- Copyright © Cambridge Philosophical Society 1961
References
REFERENCES
- 2
- Cited by


