Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jawanpuria, Pratik
Meghwanshi, Mayank
and
Mishra, Bamdev
2019.
Low-rank approximations of hyperbolic embeddings.
p.
7159.
Candellero, Elisabetta
and
Stauffer, Alexandre
2021.
Coexistence of competing first passage percolation on hyperbolic graphs.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 57,
Issue. 4,
Xiao, Meng
Qiao, Ziyue
Fu, Yanjie
Du, Yi
Wang, Pengyang
and
Zhou, Yuanchun
2021.
Expert Knowledge-Guided Length-Variant Hierarchical Label Generation for Proposal Classification.
p.
757.
Song, Mingyang
Feng, Yi
and
Jing, Liping
2022.
A Preliminary Exploration of Extractive Multi-Document Summarization in Hyperbolic Space.
p.
4505.
Peng, Wei
Varanka, Tuomas
Mostafa, Abdelrahman
Shi, Henglin
and
Zhao, Guoying
2022.
Hyperbolic Deep Neural Networks: A Survey.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
Vol. 44,
Issue. 12,
p.
10023.
Cao, Xiaofeng
and
Tsang, Ivor W.
2022.
Distribution Disagreement via Lorentzian Focal Representation.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
Vol. 44,
Issue. 10,
p.
6872.
Ma, Yuhao
Zhu, Jian
and
Liu, Jie
2022.
Enhanced semantic representation learning for implicit discourse relation classification.
Applied Intelligence,
Vol. 52,
Issue. 7,
p.
7700.
Lecca, Paola
2023.
Uncovering the geometry of protein interaction network: The case of SARS-CoV-2 protein interactome.
Vol. 2872,
Issue. ,
p.
030008.
Song, Mingyang
Feng, Yi
and
Jing, Liping
2023.
HISum: Hyperbolic Interaction Model for Extractive Multi-Document Summarization.
p.
1427.
Mettes, Pascal
Ghadimi Atigh, Mina
Keller-Ressel, Martin
Gu, Jeffrey
and
Yeung, Serena
2024.
Hyperbolic Deep Learning in Computer Vision: A Survey.
International Journal of Computer Vision,
Vol. 132,
Issue. 9,
p.
3484.
Liu, Jiaxu
Yi, Xinping
and
Huang, Xiaowei
2024.
DeepHGCN: Toward Deeper Hyperbolic Graph Convolutional Networks.
IEEE Transactions on Artificial Intelligence,
Vol. 5,
Issue. 12,
p.
6172.
Liu, Jiaxu
Yi, Xinping
Wu, Sihao
Yin, Xiangyu
Zhang, Tianle
Huang, Xiaowei
and
Jin, Shi
2024.
Machine Learning and Knowledge Discovery in Databases. Research Track.
Vol. 14943,
Issue. ,
p.
231.
Li, Lening
Luo, Lei
and
Sun, Yanguang
2025.
Pattern Recognition.
Vol. 15309,
Issue. ,
p.
276.
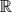 ${\mathbb R}$-tree T that reflects the geometry of X in the following sense. All rays in T are quasi-geodesic in X. Every geodesic ray in X lies eventually close to a ray of T. The embedding of T in X extends continuously to their boundaries in a finite-to-one way, the number of boundary points of T mapping to a given boundary point of X being bounded if the (Assouad) dimension of the boundary of X is finite.
${\mathbb R}$-tree T that reflects the geometry of X in the following sense. All rays in T are quasi-geodesic in X. Every geodesic ray in X lies eventually close to a ray of T. The embedding of T in X extends continuously to their boundaries in a finite-to-one way, the number of boundary points of T mapping to a given boundary point of X being bounded if the (Assouad) dimension of the boundary of X is finite.